题目内容
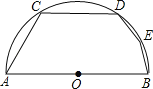
【题目】如图,在半圆中AB为直径,弦AC=CD=6![]() ,DE=EB=2,弧CDE的长度为 .
,DE=EB=2,弧CDE的长度为 .
【答案】![]()
【解析】
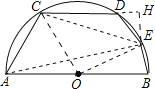
试题分析:过点E作EH⊥CD于H,连接OC、OE、AE,如图所示.根据弧、弦和圆周角的关系可得∠COE=90°,根据圆周角定理可得∠CAE=45°,再根据圆内接四边形对角互补及同角的补角相等可得∠HDE=45°,然后运用勾股定理可依次求出CE,CO,然后运用圆弧长公式就可解决问题.
解:过点E作EH⊥CD于H,连接OC、OE、AE,如图所示.
∵AC=CD,DE=EB,
∴![]() ,
,![]() ,
,
∴∠COE=![]() ∠AOB=90°,
∠AOB=90°,
∴∠CAE=45°.
∵∠CDE+∠CAE=180°,∠CDE+∠HDE=180°,
∴∠HDE=∠CAE=45°.
在Rt△DHE中,HE=DE×sin∠HDE=2×![]() =
=![]() ,
,
DH=DE×cos∠HDE=2×![]() =
=![]() .
.
在Rt△CHE中,CE=![]() =
=![]() =10.
=10.
在Rt△COE中,CO=![]() CE=5
CE=5![]() ,
,
∴弧CDE的长度为![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目