题目内容
【题目】我们知道,实数与数轴上的点是一一对应的,任意一个实数在数轴上都能找到与之对应的点,比如我们可以在数轴上找到与数字2对应的点.
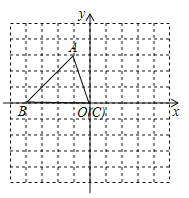
(1)在如图所示的数轴上,画出一个你喜欢的无理数,并用点![]() 表示;
表示;
(2)(1)中所取点![]() 表示的数字是______,相反数是_____,绝对值是______,倒数是_____,其到点5的距离是______.
表示的数字是______,相反数是_____,绝对值是______,倒数是_____,其到点5的距离是______.
(3)取原点为![]() ,表示数字1的点为
,表示数字1的点为![]() ,将(1)中点
,将(1)中点![]() 向左平移2个单位长度,再取其关于点
向左平移2个单位长度,再取其关于点![]() 的对称点
的对称点![]() ,求
,求![]() 的长.
的长.
![]()
【答案】(1)见解析;(2)![]() (答案不唯一);(3)
(答案不唯一);(3)![]() (答案不唯一).
(答案不唯一).
【解析】
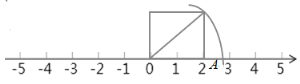
(1)先在数轴上以原点为起始点,以某个单位长度的长为边长画正方形,再连接正方形的对角线,以对角线为半径,原点为圆心画弧即可在数轴上得到一个无理数;
(2)根据(1)中的作图可得出无理数的值,然后根据相反数,绝对值,倒数的概念以及点与点间的距离概念作答;
(3)先在数轴上作出点A平移后得到的点A′,点B,点C,再利用对称性及数轴上两点间的距离的定义,可求出CO的长.
解:(1)如图所示:(答案不唯一)
(2)由(1)作图可知,点![]() 表示的数字是
表示的数字是![]() ,相反数是-
,相反数是-![]() ,绝对值是
,绝对值是![]() ,倒数是
,倒数是![]() ,其到点5的距离是5-
,其到点5的距离是5-![]() ,
,
故答案为:![]() (答案不唯一)
(答案不唯一)
(3)如图,将点![]() 向左平移2个单位长度,得到点
向左平移2个单位长度,得到点![]() ,
,
则点![]() 表示的数字为
表示的数字为![]() ,
,
![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,
![]() 点
点![]() 表示的数字为1,
表示的数字为1,
∴A′B=BC=1-(![]() )=3-
)=3-![]() ,
,
∴A′C=2A′B=6-![]() ,
,
∴CO=OA′+A′C=![]() +6-
+6-![]() =4-
=4-![]() ,
,
即CO的长为![]() .(答案不唯一)
.(答案不唯一)
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目