题目内容
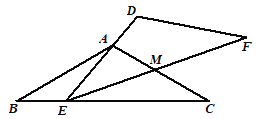
【题目】如图,在等边△ABC中,E,F分别在边AC、BC上,满足AE=CF,连接BE,AF交于点P.
(1)求证:△ABE≌△CAF;
(2)求∠APB的度数.

【答案】(1)证明见解析;(2)120°.
【解析】试题(1)根据等边三角形的性质可知∠BAC=∠C=60°,AB=CA,结合AE=CF,可证明△ABE≌△CAD(SAS);
(2)由△ABE≌△CAD可得∠ABE=∠CAF,由等式的性质可得∠ABE+∠CAF=∠CAF+∠CAF=∠BAC=60°,在△ABP中,由三角形内角和定理可求得∠APB的度数.
试题解析:(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAF中,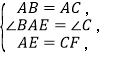
∴△ABE≌△CAF(SAS);
(2)∵△ABE≌△CAF,
∴∠ABE=∠CAF,
∴∠ABE+∠CAF=∠CAF+∠CAF=∠BAC=60°,
∴在△ABP中,∠APB=180°-(∠PBA+∠PAB)=180°-∠BAC=120°.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目