题目内容
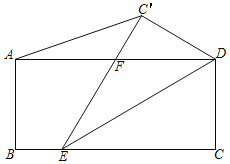
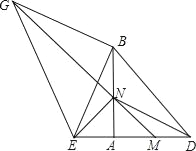
【题目】如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求![]() 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.
【答案】(1)详见解析;(2)![]() ;(3)四边形BDNG是平行四边形,证明详见解析.
;(3)四边形BDNG是平行四边形,证明详见解析.
【解析】
(1)连接BM,推出BE=BM,∠EBA=∠MBA,根据SAS证△BMN≌△BEN,推出∠BMN=∠BEN,证出∠BMN=∠BGN即可;
(2)过G作GH⊥AB,垂足为H,证△BGH≌△ABE,推出BH=AE=AN,求出NG=![]() GH=
GH=![]() AB,代入求出即可;
AB,代入求出即可;
(3)根据ADN≌△BAE,推出BG⊥BE,BG=BE,得出BG∥DN,BG=DN,根据平行四边形的判定判断即可.
(1)证明:连BM,
∵∠BAD=90°,
∴BA⊥EM,
∵AE=AM,
∴BE=BM,∠EBA=∠MBA,
在△BEN和△BMN中
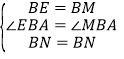 ,
,
∴△BMN≌△BEN,
∴∠BMN=∠BEN,
∵BE=BG=BM,
∴∠BMN=∠BGN,
∴∠BEN=∠BGN.
(2)解:由(1)得,∠GBE=∠GNE=90°,
∴△NME等腰直角三角形,
∴AE=AN,
过G作GH⊥AB,垂足为H,
∴∠H=∠BAE=∠GBE=90°,
∴∠HGB+∠HBG=90°,∠HBG+∠ABE=90°,
∴∠HGB=∠EBA,
在△BGH和△ABE中
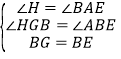 ,
,
∴△BGH≌△ABE,
∴BH=AE=AN,
HN=AB=GH,NG=![]() GH=
GH=![]() AB,
AB,
∴![]() .
.
(3)解:四边形BDNG是平行四边形,
理由是:∵∠DAN=∠BAE=90°,AN=AE,AB=AD,
∴△ADN≌△BAE,
∴DN⊥BE,DN=BE=BG,
又∵BG⊥BE,BG=BE,
∴BG∥DN,BG=DN
∴四边形BDNG为平行四边形.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案