题目内容
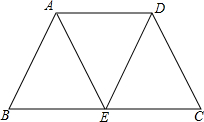
如图,已知梯形ABCD中,AD∥BC,AB=DC,将△ABE沿AE折叠刚好与△ADE重合.
(1)求证:四边形ABED是平行四边形;
(2)写出关于这个图形的另外一条正确结论.
(1)求证:四边形ABED是平行四边形;
(2)写出关于这个图形的另外一条正确结论.

(1)证明:∵梯形ABCD中,将△ABE沿AE折叠刚好与△ADE重合,
∴∠BAE=∠DAE,AB=AD,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=AD,
又BE∥AD,
∴四边形ABED是平行四边形;
(2)△DEC是等腰三角形,
证明:∵四边形ABED是平行四边形,
∴AB=DE,
∵AB=CD,
∴DC=DE,
故△DEC是等腰三角形,(答案不唯一).
∴∠BAE=∠DAE,AB=AD,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=AD,
又BE∥AD,
∴四边形ABED是平行四边形;
(2)△DEC是等腰三角形,
证明:∵四边形ABED是平行四边形,
∴AB=DE,
∵AB=CD,
∴DC=DE,
故△DEC是等腰三角形,(答案不唯一).

练习册系列答案
相关题目










