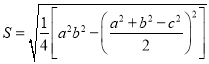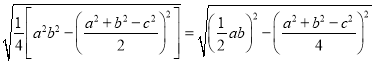题目内容
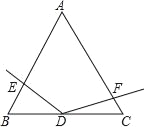
【题目】如图，在△ABC中，AB=AC，∠BAC=120°，D，E是BC上的两点，且∠DAE=30°，将△AEC绕点A顺时针旋转120°后，得到△AFB，连接DF.下列结论中正确的个数有（ ）
①∠FBD=60°；②△ABE∽△DCA；③AE平分∠CAD；④△AFD是等腰直角三角形.
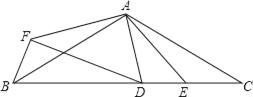
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
根据旋转的性质得出∠ABF＝∠C，求出∠ABC＝∠C＝30°，即可判断①；根据三角形外角性质求出∠ADC＝∠BAE，根据相似三角形的判定即可判断②；求出∠EAC大于30°，而∠DAE＝30°，即可判断③；求出△AFD是直角三角形，但是不能推出是等腰三角形，即可判断④．
解：∵在△ABC中，AB＝AC，∠BAC＝120°，
∴∠ABC＝∠C＝30°，
∵将△AEC绕点A顺时针旋转120°后，得到△AFB，
∴△AEC≌△AFB，
∴∠ABF＝∠C＝30°，
∴∠FBD＝30°＋30°＝60°，∴①正确；
∵∠ABC＝∠DAE＝30°，
∴∠ABC＋∠BAD＝∠DAE＋∠BAD，
即∠ADC＝∠BAE，
∵∠ABC＝∠C，
∴△ABE∽△DCA，∴②正确；
∵∠C＝∠ABC＝∠DAE＝30°，∠BAC＝120°，
∴∠BAD＋∠EAC＝120°∠DAE＝90°，
∴∠ABC＋∠BAD＜90°，
∴∠ADC＜90°，
∴∠DAC＞60°，
∴∠EAC＞30°，
即∠DAE≠∠EAC，∴③错误；
∵将△AEC绕点A顺时针旋转120°后，得到△AFB，
∴AF＝AE，∠EAC＝∠BAF，
∵∠BAC＝120°，∠DAE＝30°，
∴∠BAD＋∠EAC＝90°，
∴∠DAB＋∠BAF＝90°，
即△AFD是直角三角形，
∵在△DAE中，∠ADE＝∠ABC＋∠BAD，∠AED＝∠C＋∠EAC，∠ABC＝∠C，但是根据已知不能推出∠BAD＝∠EAC，
∴∠ADE和∠AED不相等，
∴AD和AE不相等，
即△AFD是直角三角形，但是不一定是等腰三角形，∴④错误；
故选：B．
