题目内容
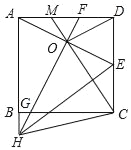
【题目】如图,正方形ABCD中,E为CD的中点,AE的垂直平分线分别交AD,BC及AB的延长线于点F,G,H,连接HE,HC,OD,连接CO并延长交AD于点M.则下列结论中:
①FG=2AO;②OD∥HE;③![]() ;④2OE2=AHDE;⑤GO+BH=HC
;④2OE2=AHDE;⑤GO+BH=HC
正确结论的个数有( )
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
建立以B点位坐标原点的平面直角坐标系,分别求出相应直线的解析式和点的坐标,求出各线段的距离,可得出结论.
解:如图,
建立以B点为坐标原点的平面直角坐标系,设正方形边长为2,可分别得各点坐标,
A(0,2),B(0,0),C(2,0),D(2,2), E为CD的中点,可得E点坐标(2,1),可得AE的直线方程,![]() ,由OF为直线AE的中垂线可得O点为
,由OF为直线AE的中垂线可得O点为![]() ,设直线OF的斜率为K,得
,设直线OF的斜率为K,得![]() ,可得k=2,同时经过点O(
,可得k=2,同时经过点O(![]() ),可得OF的直线方程:
),可得OF的直线方程:
![]() ,可得OF与x轴、y轴的交点坐标G(
,可得OF与x轴、y轴的交点坐标G(![]() ,0),H(0,
,0),H(0,![]() ),及F(
),及F(![]() ,2),
,2),
同理可得:直线CO的方程为:![]() ,可得M点坐标(
,可得M点坐标(![]() ,2),
,2),
可得:①FG=![]() ,
,
AO=![]()
![]() =
=![]() ,
,
故FG=2AO,故①正确;
②:由O点坐标![]() ,D点坐标(2,2),可得OD的方程:
,D点坐标(2,2),可得OD的方程:![]() ,
,
由H点坐标(0,![]() ),E点坐标(2,1),可得HE方程:
),E点坐标(2,1),可得HE方程:![]() ,
,
由两方程的斜率不相等,可得OD不平行于HE,
故②错误;
③由A(0,2),M(![]() ,2),H(0,
,2),H(0,![]() ),E(2,1),
),E(2,1),
可得:BH=![]() ,EC=1,AM=
,EC=1,AM=![]() ,MD=
,MD=![]() ,
,
故![]() =
=![]() ,
,
故③正确;
④:由O点坐标![]() ,E(2,1),H(0,
,E(2,1),H(0,![]() ),D(2,2),
),D(2,2),
可得:![]() ,
,
AH=![]() ,DE=1,
,DE=1,![]() 有2OE2=AHDE,
有2OE2=AHDE,
故④正确;
⑤:由G(![]() ,0),O点坐标
,0),O点坐标![]() ,H(0,
,H(0,![]() ),C(2,0),
),C(2,0),
可得:![]() ,
,
BH=![]() ,HC=
,HC=![]() ,
,
可得:GO≠BH+HC,
故正确的有①③④,
故选B.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目