ƒøƒ⁄»ð
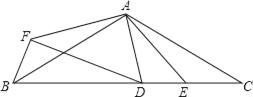
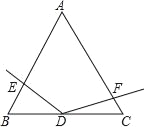
°æƒø°ø»ÁÕº£¨°˜ABC «±þ≥§Œ™4µƒµ»±þ»˝Ω«–Œ£¨µ„D «œþ∂ŒBCµƒ÷–µ„£¨°œEDF£Ω120°„£¨∞—
°œEDF»∆µ„D–˝◊™£¨ π°œEDFµƒ¡Ω±þ∑÷±”Îœþ∂ŒAB°¢ACΩª”⁄µ„E°¢F£Æ
£®1£©µ±DF°ÕAC ±£¨«Û÷§£∫BE£ΩCF£ª
£®2£©‘⁄–˝◊™π˝≥Ã÷–£¨BE+CF «∑ÒŒ™∂®÷µ£ø»Ù «£¨«Û≥ˆ’‚∏ˆ∂®÷µ£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©‘⁄–˝◊™π˝≥Ã÷–£¨¡¨Ω”EF£¨…ËBE£Ωx£¨°˜DEFµƒ√ʪ˝Œ™S£¨«ÛS”Îx÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«ÛSµƒ◊Ó–°÷µ£Æ
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©BE+CF£Ω2£¨ «Œ™∂®÷µ£ª£®3£©S£Ω![]() £®x©Å1£©2
£®x©Å1£©2![]() £¨µ±x£Ω1 ±£¨S◊Ó–°÷µŒ™
£¨µ±x£Ω1 ±£¨S◊Ó–°÷µŒ™![]() .
.
°æΩ‚Œˆ°ø
£®1£©∏˘æðÀƒ±þ–Œƒ⁄Ω«∫ÕŒ™360°„£¨ø…«Û°œDEA£Ω90°„£¨∏˘æð°∞AAS°±ø…≈–∂®°˜BDE°’°˜CDF£¨º¥ø…÷§BE£ΩCF£ª
£®2£©π˝µ„D◊˜DM°ÕAB”⁄M£¨◊˜DN°ÕAC”⁄N£¨»ÁÕº2£¨“◊÷§°˜MBD°’°˜NCD£¨‘Ú”–BM£ΩCN£¨DM£ΩDN£¨Ω¯∂¯ø…÷§µΩ°˜EMD°’°˜FND£¨‘Ú”–EM£ΩFN£¨æÕø…µ√µΩBE+CF£ΩBM+EM+CF£ΩBM+FN+CF£ΩBM+CN£Ω2BM£Ω2BD°¡cos60°„£ΩBD£Ω![]() BC£Ω2£ª
BC£Ω2£ª
£®3£©π˝µ„F◊˜FG°ÕAB£¨”…“‚ø…µ√S°˜DEF£ΩS°˜ABC©ÅS°˜AEF©ÅS°˜BDE©ÅS°˜BCF£¨‘Úø…«ÛS”Îx÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£¨∏˘æð∂˛¥Œ∫Ø ˝◊Ó÷µµƒ«Û∑®£¨ø…«ÛSµƒ◊Ó–°÷µ£Æ
£®1£©°þ°˜ABC «±þ≥§Œ™4µƒµ»±þ»˝Ω«–Œ£¨µ„D «œþ∂ŒBCµƒ÷–µ„£¨
°ý°œB£Ω°œC£Ω60°„£¨BD£ΩCD£¨
°þDF°ÕAC£¨
°ý°œDFA£Ω90°„£¨
°þ°œA+°œEDF+°œAFD+°œAED£Ω180°„£¨
°ý°œAED£Ω90°„£¨
°ý°œDEB£Ω°œDFC£¨«“°œB£Ω°œC£Ω60°„£¨BD£ΩDC£¨
°ý°˜BDE°’°˜CDF£®AAS£©
£®2£©π˝µ„D◊˜DM°ÕAB”⁄M£¨◊˜DN°ÕAC”⁄N£¨
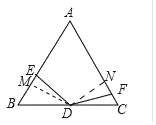
‘Ú”–°œAMD£Ω°œBMD£Ω°œAND£Ω°œCND£Ω90°„£Æ
°þ°œA£Ω60°„£¨
°ý°œMDN£Ω360°„©Å60°„©Å90°„©Å90°„£Ω120°„£Æ
°þ°œEDF£Ω120°„£¨
°ý°œMDE£Ω°œNDF£Æ
‘⁄°˜MBD∫Õ°˜NCD÷–£¨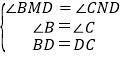
°ý°˜MBD°’°˜NCD£®AAS£©
BM£ΩCN£¨DM£ΩDN£Æ
‘⁄°˜EMD∫Õ°˜FND÷–£¨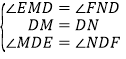 £¨
£¨
°ý°˜EMD°’°˜FND£®ASA£©
°ýEM£ΩFN£¨
°ýBE+CF£ΩBM+EM+CF£ΩBM+FN+CF£ΩBM+CN
£Ω2BM£Ω2BD°¡cos60°„£ΩBD£Ω![]() BC£Ω2
BC£Ω2
£®3£©π˝µ„F◊˜FG°ÕAB£¨¥π◊„Œ™G£¨
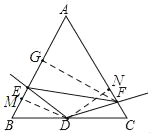
°þBE£Ωx
°ýAE£Ω4©Åx£¨CF£Ω2©Åx£¨
°ýAF£Ω2+x£¨
°þS°˜DEF£ΩS°˜ABC©ÅS°˜AEF©ÅS°˜BDE©ÅS°˜BCF£¨
°ýS£Ω![]() BC°¡AB°¡sin60°„©Å
BC°¡AB°¡sin60°„©Å![]() AE°¡AF°¡sin60°„©Å
AE°¡AF°¡sin60°„©Å![]() BE°¡BD°¡sin60°„©Å
BE°¡BD°¡sin60°„©Å![]() CF°¡CD°¡sin60°„
CF°¡CD°¡sin60°„
£Ω4![]() ©Å
©Å![]() °¡£®4©Åx£©°¡£®2+x£©°¡
°¡£®4©Åx£©°¡£®2+x£©°¡![]() ©Å
©Å![]() °¡x°¡2°¡
°¡x°¡2°¡![]() ©Å
©Å![]() °¡£®2©Åx£©°¡2°¡
°¡£®2©Åx£©°¡2°¡![]()
°ýS£Ω![]() £®x©Å1£©2+
£®x©Å1£©2+![]() £®
£®
°ýµ±x£Ω1 ±£¨S◊Ó–°÷µŒ™![]()

 Ω◊Ãðº∆À„œµ¡–¥∞∏
Ω◊Ãðº∆À„œµ¡–¥∞∏