题目内容
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
【答案】20.
【解析】
试题根据题意画出图形,利用勾股定理建立方程,求出x的值即可.
试题解析:画图解决,通过建模把距离转化为线段的长度.
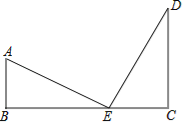
由题意得:AB=20,DC=30,BC=50,设EC为x肘尺,BE为(50﹣x)肘尺,
在Rt△ABE和Rt△DEC中,![]() ,
,![]() ,
,
又∵AE=DE,∴![]() ,解得:
,解得:![]() ,
,
答:这条鱼出现的地方离比较高的棕榈树的树根20肘尺.

练习册系列答案
相关题目