题目内容
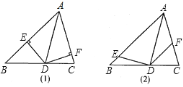
【题目】△ABC是⊙O的内接三角形,BC= ![]() .如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=
.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA= ![]() BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 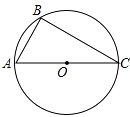
【答案】解:图形如图所示,直线l与⊙O相切. 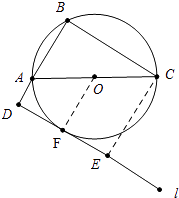
理由:作OF⊥l于F,CE⊥l于E,
∵AC是直径,
∴∠ABC=90°,
∵l⊥BD,
∴∠BDE=90°,
∵OF⊥l,CE⊥l,
∴AD∥OF∥CE,
∵AO=OC,
∴DF=FE,
∴OF= ![]() (AD+CE),
(AD+CE),
设AD=a,则AB=2AD=2a,
∵∠ABC=∠BDE=∠CED=90°,
∴四边形BDEC是矩形,
∴CE=BD=3a,
∴OF=2a,
∵在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2a,
∴AC=4a,
∴OF=OA=2a,
∴直线l是⊙O切线
【解析】作OF⊥l于F,CE⊥l于E,设AD=a,则AB=2AD=2a,只要证明OF是梯形ADEC的中位线即可解决问题.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目