Question

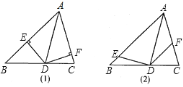
【题目】如图，在等腰Rt△ABC中，斜边AB=8，点P在以AC为直径的半圆上，M为PB的中点，当点P沿半圆从点A运动至点C时，点M运动的路径长是（ ）
A.2 π
B. π
C.2π
D.2

Answer 1

【答案】B
【解析】解：如图，连接PA、PC，取AB、BC的中点E、F，连接EF、EM、FM．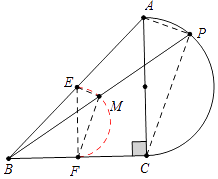
∵AC是直径，
∴∠APC=90°，
∵BE=EA，BM=MP，
∴EM∥PA，同理FM∥PC，
∴∠BME=∠BPA，∠BMF=∠BPC，
∴∠BME+∠BMF=∠BPA+∠BPC=90°，
∴∠EMF=90°，
∴点M的轨迹是 ，（EF为直径的半圆，图中红线部分）
∵BC=AC，∠ACB=90°，AB=8，
∴AC=4 ，EF= AC=2 ，
∴ 的长=π = π．
故选B．
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)．