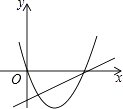Question

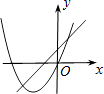
【题目】将一根长为6cm的木棍分成两段，每段长分别为a，b（单位：cm）且a，b都为正整数．在直角坐标系中以a，b的值，构成点A（a，b）．那么点A落在抛物线y=﹣x2+6x﹣5与x轴所围成的封闭图形内部（如图，不含边界）的概率为 ．

Answer 1

【答案】
【解析】解：根据题意A的坐标共有5种情况：（1，5），（2，4），（3，3），（4，2），（5，1） 当x=1时，y=﹣x2+6x﹣5=0，（1，5）没在内部，
x=2时，y=﹣x2+6x﹣5=3，（2，4）没在内部，
x=3时，y=﹣x2+6x﹣5=4，（3，3）在内部，
x=4时，y=﹣x2+6x﹣5=3，（4，2）在内部，
x=5时，y=﹣x2+6x﹣5=0，（5，1）没有在内部，
所以，在封闭图形内部的点有1个，
P= ．
所以答案是 ．
【考点精析】根据题目的已知条件，利用二次函数的性质和概率公式的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n．