题目内容
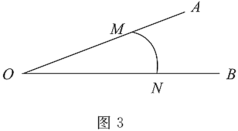
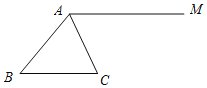
【题目】如图,AM∥BC,且AC平分∠BAM.
(1)用尺规作∠ABC的平分线BD交AM于点D,连接CD.(只保留作图痕迹,不写作法)
(2)求证:四边形ABCD是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用尺规作图的方式(本质为三角形全等)作出∠ABC的角平分线即可;
(2)先证明AB=BC,AB=AD,则AD=BC,则可判断四边形ABCD是平行四边形,然后加上邻边相等可判断四边形ABCD是菱形.
解:(1)如下图所示,DB、CD为所作;
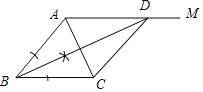
(2)证明:∵AC平分∠BAM,
∴∠BAC=∠DAC,
∵AM∥BC,
∴∠DAC=∠BCA.
∴∠BAC=∠BCA.
∴AB=BC,
同理可证:AB=AD.
∴AD=BC.
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴四边形ABCD是菱形.

练习册系列答案
相关题目