题目内容
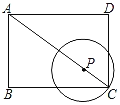
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为__.
【答案】![]() 或
或![]()
【解析】
作PE⊥AD于E,PF⊥AB于F,根据勾股定理求出AC,分⊙P与AD相切、⊙P与AB相切相切两种情况,根据相似三角形的判定定理和性质定理计算.
解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC=![]() =5,
=5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE//CD,
∴△APE∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CP=![]() ,
,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF//BC,
∴△APE∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CP=![]() ,
,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表:
甲的体温 | 乙的体温 | 丙的体温 | ||||||||||||
温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 |
频数 | 5 | 5 | 5 | 5 | 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 |
则在这20天中,甲、乙、丙三名同学的体温情况最稳定的是________.
【题目】某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表.下面有四个推断:
初一年级植树情况统计表 | |||||
棵树/棵 | 1 | 2 | 3 | 4 | 5 |
人数 | 7 | 33 | a | 12 | 3 |
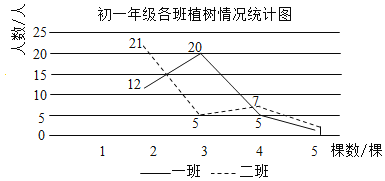
①a的值为20;
②初一年级共有80人;
③一班植树棵树的众数是3;
④二班植树棵树的是中位数2.
其中合理的是( )
A.①③B.②④C.②③D.②③④