Question

【题目】已知：在平面直角坐标系xOy中，函数y＝（n≠0，x＞0）的图象过点A（3，2），与直线l：y＝kx+b交于点C，直线l与y轴交于点B（0，﹣1）．

（1）求n、b的值；

（2）横、纵坐标都是整数的点叫做整点．记函数y＝（n≠0，x＞0）的图象在点A，C之间的部分与线段BA，BC围成的区域（不含边界）为W．

①当直线l过点（2，0）时，直接写出区域W内的整点个数，并写出区域W内的整点的坐标；

②若区域W内的整点不少于5个，结合函数图象，求k的取值范围．

Answer 1

【答案】（1）n＝6，b＝﹣1；（2）①（3，1），②0＜k＜或k＞5

【解析】

（1）把A（3，2）代入y＝（n≠0，x＞0）中可得n的值；把点B（0，﹣1）代入y＝kx+b中可得b的值；

（2）①将（2，0）代入y＝kx﹣1可得：直线解析式为y＝x﹣1，画图可得整点的个数；

②分两种情况：直线l在OA的下方和上方，画图计算边界时k的值，可得k的取值．

解：（1）∵点A（3，2）在函数的图象上，

∴n＝6，

∵点B（0，﹣1）在直线l：y＝kx+b上，

∴b＝﹣1；

（2）①当直线l过点（2，0）时，直线解析式为y＝x﹣1，

解方程＝x﹣1得x1＝1﹣（舍去），x2＝1+，则C（1+，），

而B（0，﹣1），

如图1所示，区域W内的整点有（3，1）一个；

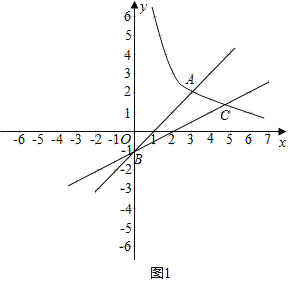
②（ⅰ）当直线l在BA下方时，

若直线l与x轴交于点（3，0），结合图象，区域W内有4个整点，

此时：3k﹣1＝0，

∴．

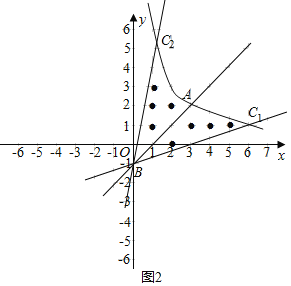
当直线l与x轴的交点在（3，0）右侧时，区域W内整点个数不少于5个，

∴0＜k＜．

（ⅱ）当直线l在BA上方时，若直线l过点（1，4），结合图象，区域W内有4个整点，

此时k﹣1＝4，解得 k＝5．

结合图象，可得 k＞5时，区域W内整点个数不少于5个，

综上，k的取值范围是0＜k＜或k＞5．