题目内容
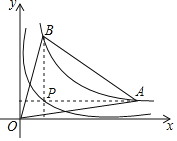
【题目】如图,AC是⊙O的弦,AC=6,点B是⊙O上的一个动点,且∠ABC=60°,若点M、N分别是AC、BC的中点,则MN的最大值是_____.

【答案】2![]() .
.
【解析】
作直径AD,如图,先判断NM为△CAB的中位线得到MN=![]() AB,再根据圆周角定理得到∠ACD=90°,利用含30度的直角三角形三边的关系得到AD=4
AB,再根据圆周角定理得到∠ACD=90°,利用含30度的直角三角形三边的关系得到AD=4![]() ,由于AB=AD时,AB的值最大,从而得到MN的最大值.
,由于AB=AD时,AB的值最大,从而得到MN的最大值.
解:作直径AD,如图,
∵点M、N分别是AC、BC的中点,
∴NM为△CAB的中位线,
∴MN=![]() AB,
AB,
∵AD为直径,
∴∠ACD=90°,
∵∠ADC=∠ABC=60°
∴CD=![]() AC=2
AC=2![]() ,
,
AD=2CD=4![]() ,
,
当AB=AD时,AB的值最大,
∴AB最大值为4![]() ,MN的最大值为2
,MN的最大值为2![]() .
.
故答案为:2![]() .
.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案【题目】某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表.下面有四个推断:
初一年级植树情况统计表 | |||||
棵树/棵 | 1 | 2 | 3 | 4 | 5 |
人数 | 7 | 33 | a | 12 | 3 |
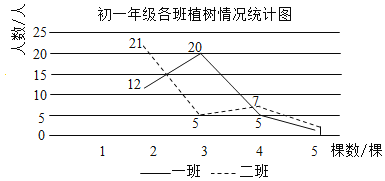
①a的值为20;
②初一年级共有80人;
③一班植树棵树的众数是3;
④二班植树棵树的是中位数2.
其中合理的是( )
A.①③B.②④C.②③D.②③④
【题目】某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量 垃圾种类(吨) | “厨余垃圾”箱 | “可回收物”箱 | “有害垃圾”箱 | “其他垃圾”箱 |
厨余垃圾 | 400 | 100 | 40 | 60 |
可回收物 | 30 | 140 | 10 | 20 |
有害垃圾 | 5 | 20 | 60 | 15 |
其他垃圾 | 25 | 15 | 20 | 40 |

下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为![]() ;
;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.其中正确的个数是( )
A.0B.1C.2D.3