��Ŀ����
����Ŀ�����![]() �������˵�
�������˵�![]() �ֱ���
�ֱ���![]() ��������(�����
��������(�����![]() �غ�)������
�غ�)������![]() ���˵�������е㶼��
���˵�������е㶼��![]() ���ڲ������
���ڲ������![]() ��
��![]() �ġ����ǻ�����
�ġ����ǻ�����
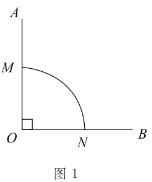
(1)ͼ1�У�![]() ��ֱ�ǣ�
��ֱ�ǣ�![]() ����
����![]() ΪԲ�ģ��뾶Ϊ1�ġ����ǻ�����
ΪԲ�ģ��뾶Ϊ1�ġ����ǻ�����
��ͼ��![]() �ij���______������ͼ������һ����
�ij���______������ͼ������һ����![]() Ϊ�˵㡢������ͬ�ġ����ǻ�����
Ϊ�˵㡢������ͬ�ġ����ǻ�����
����![]() Ϊ�˵㣬������ġ����ǻ����ij�����_______��
Ϊ�˵㣬������ġ����ǻ����ij�����_______��
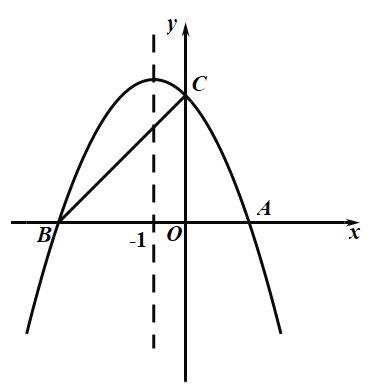
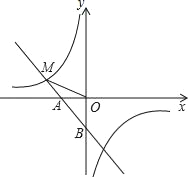
(2)��ͼ2����ƽ��ֱ������ϵ![]() �У���
����![]() ����
����![]() ��
��![]() ���������ϣ���
���������ϣ���![]() �ǰ�Բ��Ҳ��
�ǰ�Բ��Ҳ��![]() �������ǻ�������
�������ǻ�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��

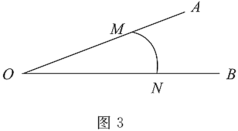
(3)��ͼ3����֪��![]() �ֱ�������
�ֱ�������![]() �ϣ�
�ϣ�![]() ��
��![]() �ġ����ǻ�������
�ġ����ǻ�������![]() ����Բ�İ뾶Ϊ
����Բ�İ뾶Ϊ![]() ��ֱ��д��
��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�(1) ��![]() ����ͼ����������
����ͼ����������![]() ��(2) 1��t��3��(3) 0��<��AOB��30����
��(2) 1��t��3��(3) 0��<��AOB��30����
��������
(1) �ٸ��ݻ�����ʽ���㣬���ɵõ��𰸣���ON��OMΪ�߳���������OMHN������HΪԲ�ģ�OMΪ�뾶���������ɵõ����ڸ���ֱ�����ԵĻ���������㼴�ɵõ��𰸣�
(2)��MN��ֱx�ύx����N��ʱ����ʱt��С����MN��ֱONʱ����ʱt�������������ֱ����t���ɵõ�t�ķ�Χ��
(3)��OM��MNʱ��ȡ���Ƕ����ֵ�����������ǶȵĴ�С���ɵõ��𰸣�
(1) �ٸ��ݻ�����ʽ�õ���![]() ��
��
��ON��OMΪ�߳���������OMHN������HΪԲ�ģ�OMΪ�뾶�������õ�һ����![]() Ϊ�˵㡢������ͬ�ġ����ǻ�������ͼ���£�
Ϊ�˵㡢������ͬ�ġ����ǻ�������ͼ���£�
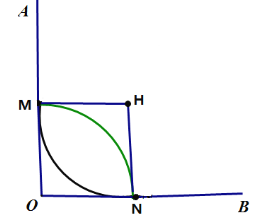
��![]() Ϊ�˵㣬ȡ�û�����������ǻ���ʱ������Բ��OA,��OB�ֱ������ڵ�M,N��ʱ��
Ϊ�˵㣬ȡ�û�����������ǻ���ʱ������Բ��OA,��OB�ֱ������ڵ�M,N��ʱ��
��OM=ON=1��
��![]() ��
��
����![]() Ϊ�˵㣬������������ǻ����ij�����
Ϊ�˵㣬������������ǻ����ij�����![]() ��
��
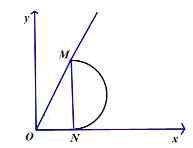
(2)��MN��ֱx�ύx����N��ʱ����ʱt��С�����N��������MN����ֱ������![]() �ǰ�Բ��������ͼȡ����Сֵ��
�ǰ�Բ��������ͼȡ����Сֵ��
��![]() ��
��
��![]() ��������MON=60����
��������MON=60����
��ON=1��ֱ��������30�����Ե�ֱ�DZߵ���б�ߵ�һ�룩��
����ʱt=1��
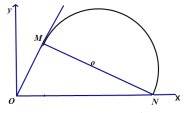
��MN��ֱONʱ����ʱt������N�����ң���![]() �Dz��ǰ�Բ����ͼtȡ�����ֵ��
�Dz��ǰ�Բ����ͼtȡ�����ֵ��
��![]() ��
��
��![]() ��������MON=30����
��������MON=30����
��ON=4��ֱ��������30�����Ե�ֱ�DZߵ���б�ߵ�һ�룩��
���ϣ�t�ķ�Χ��1��t��4��
(3) 0��<��AOB��30��

����Ŀ��ij��ס��ҡ�������ͬѧ20����������ݼ�¼���±���
������ | �ҵ����� | �������� | ||||||||||||
�¶ȣ��棩 | 36.1 | 36.4 | 36.5 | 36.8 | �¶ȣ��棩 | 36.1 | 36.4 | 36.5 | 36.8 | �¶ȣ��棩 | 36.1 | 36.4 | 36.5 | 36.8 |
Ƶ�� | 5 | 5 | 5 | 5 | Ƶ�� | 6 | 4 | 4 | 6 | Ƶ�� | 4 | 6 | 6 | 4 |
������20���У��ס��ҡ�������ͬѧ������������ȶ�����________��