Question

【题目】观察猜想：

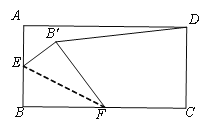
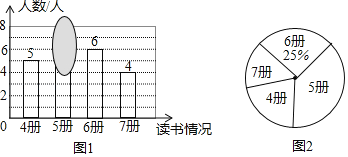
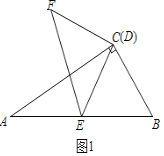
（1）如图1，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，点D与点C重合，点E在斜边AB上，连接DE，且DE＝AE，将线段DE绕点D顺时针旋转90°得到线段DF，连接EF，则＝______，sin∠ADE＝________，

探究证明：

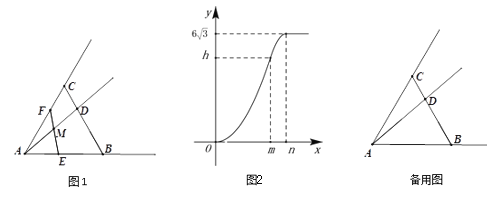
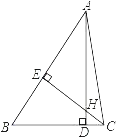
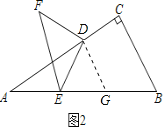
（2）在（1）中，如果将点D沿CA方向移动，使CD＝AC，其余条件不变，如图2，上述结论是否保持不变？若改变，请求出具体数值：若不变，请说明理由．

拓展延伸

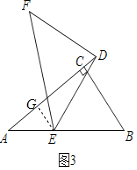
（3）如图3，在△ABC中，∠ACB＝90°，∠CAB＝a，点D在边AC的延长线上，E是AB上任意一点，连接DE．ED＝nAE，将线段DE绕着点D顺时针旋转90°至点F，连接EF．求和sin∠ADE的值分别是多少？（请用含有n，a的式子表示）

Answer 1

【答案】（1）；；（2）不变；（3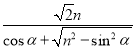）＝；sin∠ADE＝．

【解析】

（1）由等腰三角形的性质和等边三角形的判定得到∠A＝∠ACE＝30°，△BEC是等边三角形，据此求得CE的长度，根据等腰直角三角形的性质来求EF的长度，易得答案；

（2）不变．理由：如图2，过点D作DG∥BC交AB于点G，构造直角三角形：△ADG，结合含30度角的直角三角形的性质和锐角三角函数的定义，结合方程求得答案；

（3）如图3，过点E作EG⊥AD于点G，构造直角三角形，根据锐角三角函数的定义列出方程并解答．

（1）如图1，∵在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，

∴∠B＝60°．

又CE＝AE，

∴∠ACE＝∠A＝30°，

∴∠BCE＝60°，

∴△BEC是等边三角形，

∴BE＝CE．

∴AE＝CE＝BE．

∴AD＝AB＝CE．

又由旋转的性质知：FC＝EC，∠FCE＝90°，

∴EF＝CE，

∴＝＝．

∵∠ADE＝30°，

∴sin∠ADE＝．

故答案是：；；

（2）不变，理由：

如图2，过点D作DG∥BC交AB于点G，则△ADG是直角三角形．

∵∠DAG＝30°，DE＝AE，设DG＝x，

∴∠AED＝30°，AD＝x，∠DEG＝∠DGE＝60°．

∴DE＝DF＝x，sin∠ADE＝．

∵∠EDF＝90°，

∴EF＝x．

∴＝＝．

∵∠ADE＝30°，

∴sin∠ADE＝．

（3）过点E作EG⊥AD于点G，设AE＝x，则DE＝nx．

∵∠CAB＝a，

∴AG＝cosαx，EG＝sinαx．

∴DG＝＝x．

∴AD＝cosαx+x．

∵∠EDF＝90°，DE＝DF，

∴EF＝DE＝nx．

∴＝＝，

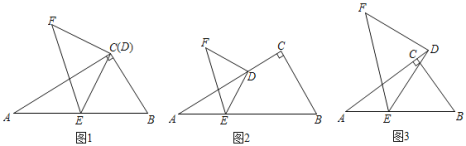
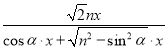sin∠ADE＝＝＝．