题目内容
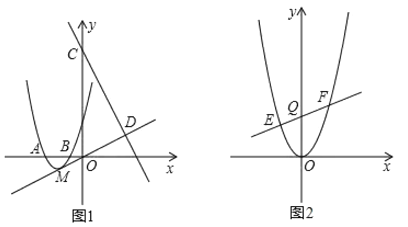
【题目】如图(1),抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图(2),将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=x2+4x+3;(2) h=4或![]() ≤h<
≤h<![]() ;(3)y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
;(3)y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
【解析】
(1)将A(-3,0)、B(-1,0),代入y=ax2+bx+3求出即可,再利用平方法求出顶点坐标即可;
(2)配方后即可确定其顶点坐标,然后利用平移规律确定函数的解析式,然后根据线段与抛物线有唯一的公共点求得h的值或取值范围即可;
(3)将抛物线平移,当顶点至原点时,其解析式为y=x2,设MN的解析式为y=kx+3(k≠0).假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过M,N作GH的垂线,垂足为G,H.根据△PMN的内心在y轴上,得到∠GMP=∠MPQ=∠QPN=∠HNP,从而△GMP∽△HNP,利用相似三角形对应边成比例即可列出有关t的方程求解即可.
(1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点
∴9a-3b+3=0且a-b+3=0
解得a=1,b=4
∴抛物线的解析式为y=x2+4x+3
(2)由(1)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,-1)
∴直线OM的解析式为y=![]() x
x
于是设平移的抛物线的顶点坐标为(h,![]() h),
h),
∴平移的抛物线解析式为y=(x-h)2+![]() h,.
h,.
①当抛物线经过点E时,
∵C(0,9),
∴h2+![]() h=9,
h=9,
解得h=![]() .
.
∴当![]() ≤h<
≤h<![]() 时,平移的抛物线与线段EF只有一个公共点.
时,平移的抛物线与线段EF只有一个公共点.
②当抛物线与线段CD只有一个公共点时,
由方程组y=(x-h)2+![]() h,y=-2x+9.
h,y=-2x+9.
得x2+(-2h+2)x+h2+![]() h-9=0,
h-9=0,
∴△=(-2h+2)2-4(h2+![]() h-9)=0,
h-9)=0,
解得h=4.
此时抛物线y=(x-4)2+2与线段CD唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与线段CD只有一个公共点时,顶点横坐标的值或取值范围是h=4或![]() ≤h<
≤h<![]() .
.
(3)将抛物线平移,当顶点至原点时,其解析式为y=x2,
设EF的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.
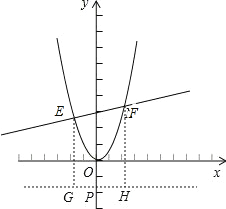
∵△PEF的内心在y轴上,
∴∠GEP=∠EPQ=∠QPF=∠HFP,
∴△GEP∽△HFP,
∴![]() ,
,
∴![]()
∴2kxExF=(t-3)(xE+xF)
由y=x2,y=kx+3.得x2-kx-3=0.
∴xE+xF=k,xExF=-3.
∴2k(-3)=(t-3)k,
∵k≠0,
∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.