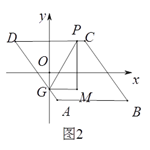题目内容
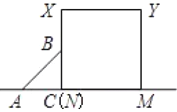
【题目】已知,如图等腰直角![]() 沿MN所在的直线以
沿MN所在的直线以![]() 的速度向右作匀速直线运动,若
的速度向右作匀速直线运动,若![]() ,则
,则![]() 和正方形
和正方形![]() 重叠部分的面积
重叠部分的面积![]() 与匀速运动所有的时间
与匀速运动所有的时间![]() 之间函数的大致图像是( )
之间函数的大致图像是( )
A.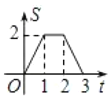 B.
B.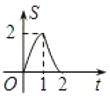 C.
C.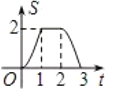 D.
D.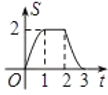
【答案】D
【解析】
分0<t<1时,1≤t≤2时,2<t≤3时三种情况,分别求出函数解析式,判断出相应的函数图象,找出符合条件的选项即可.
解:∵△ABC的运动速度是2cm/min,MN=2AC=4cm,
∴2÷2=1min,4÷2=2min,(4+2)÷2=3min,
分情况讨论:
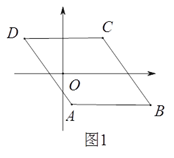
如图1,当0<t<1时,重叠部分为梯形,由图形得:AN=2-2t,NC=2t,
则面积![]() ,函数图象为开口向下的抛物线的一部分,且y随x的增大而增大,
,函数图象为开口向下的抛物线的一部分,且y随x的增大而增大,
如图2,当1≤t≤2时,重叠部分为△ABC,面积y=![]() ×2×2=2,函数图象为平行x轴的一条线段,
×2×2=2,函数图象为平行x轴的一条线段,
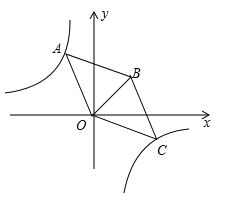
如图3,当2<t≤3时,重叠部分是三角形,由图形得:AM=![]() ,
,
则面积![]() ,函数图象为开口向上的抛物线的一部分,且y随x的增大而减小,
,函数图象为开口向上的抛物线的一部分,且y随x的增大而减小,
纵观各选项,只有D选项符合.
故选:D.
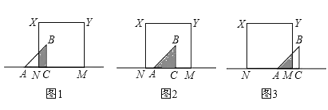

 阅读快车系列答案
阅读快车系列答案【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
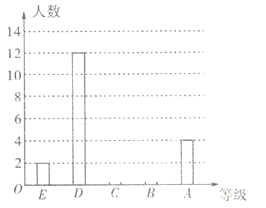
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
【题目】小西红柿又叫圣女果,既可以生吃,也可以作为美食原料,营养价值极高,因此深受人们的欢迎,为了解甲、乙两个规模相当的种植基地的小西红柿产量,从这两个种植基地中各随机选取50株小西红柿秧苗进行调查,将得到的数据分类整理成如下统计表:
甲基地每株秧苗收获小西红柿个数统计表:
小西红柿个数x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 4 | 8 | 12 | 12 | 10 | 4 |
乙基地每株秧苗收获小西红柿个数统计表:
小西红柿个数 x/个 | 25≤x<35 | 35≤x<45 | 45≤x<55 | 55≤x<65 | 65≤x<75 | 75≤x<85 |
秧苗株数/株 | 9 | 6 | 12 | 10 | 11 | 2 |
(说明:x<45为产量不合格,x≥45为产量合格,其中45≤x<65为产量良好,65≤x<85为产量优秀)
(
(2)某水果商准备在甲、乙两个小西红柿种植基地中选择一个进行合作,若一株秧苗产量优秀可获利13元,产量良好可获利8元,产量不合格亏损5元.以这两个基地的50株秧苗获得的平均利润为决策依据,请你利用所学的统计知识帮该水果商选择与哪个基地进行合作能获得更大利润?并说明理由.