题目内容
【题目】平面内有三点A(2,2![]() ),B(5,2
),B(5,2![]() ),C(5,
),C(5,![]() )
)
(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移![]() 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标.
【答案】(1)D(2,![]() );(2)s≈4.24;(3) A'(4,-
);(2)s≈4.24;(3) A'(4,-![]() )B'(7,-
)B'(7,-![]() )C'(7,-2
)C'(7,-2![]() ) D'(4,-2
) D'(4,-2![]() ).
).
【解析】
(1)抓住矩形的特点,即对边平行,邻边互相垂直的性质,AB∥DC,AB⊥AD,BC∥AD,BC⊥DC及平行线的性质,第三条直线与平行线中的任何一条平行,那么,它与另一条也平行.
(2)根据两点间的距离公式求出边长,再根据矩形的面积公式求出面积.
(3)根据平移及点的移动规律即可得解.
(1)由题意知,四边形ABCD是矩形,如图,
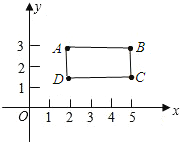
∴AB∥DC,
又∵AB平行于x轴(由AB两点的坐标可知),
∴DC也平行于x轴(平行线的性质),
∵AB⊥AD,
∴AD垂直于x轴.
∴D点既在经过C(5,![]() )平行于x轴的平行线DC上,又在经过A(2,2
)平行于x轴的平行线DC上,又在经过A(2,2![]() )的x轴的垂线AD上,
)的x轴的垂线AD上,
∴D(2,![]() );
);
(2)由题意可知:AB=5-2=3,
AD=![]() ,
,
故四边形ABCD的面积是AB×AD=3![]() ≈4.24;
≈4.24;
(3)∵四边形ABCD向右平移2个单位,再向下平移3![]() 个单位,
个单位,
∴A(2+2,2![]() -3
-3![]() ),B(5+2,2
),B(5+2,2![]() -3
-3![]() ),C(5+2,
),C(5+2,![]() -3
-3![]() ),D(2+2,
),D(2+2,![]() -3
-3![]() ),
),
即A(4,-![]() ),B(7,-
),B(7,-![]() ),C(7,-2
),C(7,-2![]() ),D(4,-2
),D(4,-2![]() ).
).

练习册系列答案
相关题目