题目内容
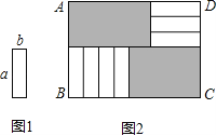
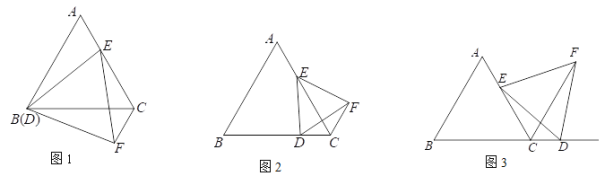
【题目】△ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE为边作等边△DEF,连接CF.
(1)如图1,当点D与点B重合时,求证:△ADE≌△CDF;
(2)如图2,当点D运动到如图2的位置时,猜想CE、CF、CD之间的数量关系,并说明理由;
(3)如图3,当点D在BC延长线上时,直接写出CE、CF、CD之间的数量关系,不证明.
【答案】(1)证明见解析;(2)CE=CD+CF,证明见解析;(3)CF=CD+CE.
【解析】
(1)利用等边三角形的性质可得AB=BC,DE=DF,由∠ABC=∠EDF=60°,∠EBC为公共角,得∠ADE=∠CDF,根据SAS得证△ADE≌△CDF.
(2)CE=CF+CD,理由为:过D作DG∥AB,交AC于点G,连接CF,如图,由DG与AB平行,利用两直线平行同位角相等,确定出三角形GDC为等边三角形,再由三角形EDF为等边三角形,利用等边三角形的性质得到两对边相等,再利用等式的性质得到夹角相等,利用SAS得到三角形EGD与三角形FCD全等,利用全等三角形对应边相等得到EG=FC,由EC=EG+GC,等量代换即可得证;
(3)CF=CE+CD,过D作DG∥AB,交AC的延长线于点G,只要证明△EGD≌△FCD即可解决问题;
(1) ∵△ABC和△DEF是等边三角形,
∴AB=BC,DE=DF,
∠ABC=∠EDF=60° ,
∴∠ADE=∠CDF ,
∴△ADE≌△CDF ,
(2)CE=CD+CF ,理由为:
证明:过D作DG∥AB,交AC于点G,连接CF,
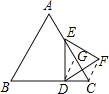
∵DG∥AB,
∴∠CGD=∠CDG=60°,△CDG为等边三角形,
∵△DEF为等边三角形,
∴∠EDF=∠GDC=60°,ED=FD,GD=CD,
∴∠EDF-∠GDF=∠GDC-∠GDF,即∠EDG=∠FDC,
在△EDG和△FDC中,
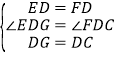 ,
,
∴△EDG≌△FDC(SAS),
∴EG=FC,
则CE=CG+EG=CG+CF=CF+CD;
(3) CF=CD+CE .

【题目】某校在一次广播操比赛中,初二 (1)班、初二(2)班、初二(3)班的各项得分如下:
服装统一 | 动作整齐 | 动作准确 | |
初二(1)班 |
|
|
|
初二(2)班 |
|
|
|
初二(3)班 |
|
|
|
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是________;在动作整齐方面三个班得分的众数是________;在动作准确方面最有优势的是________班.
(2)如果服装统一、动作整齐、动作准确三个方面的重要性之比为![]() ,那么这三个班的排名顺序怎样?为什么?
,那么这三个班的排名顺序怎样?为什么?
(3)在(2)的条件下,你对三个班级中排名最靠后的班级有何建议?