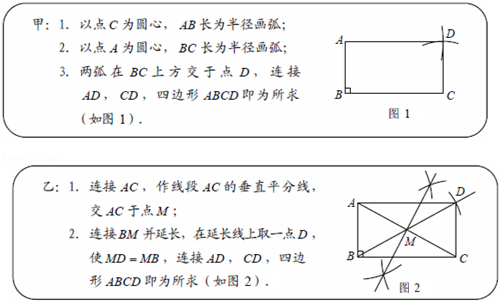
题目内容
【题目】在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“湘一点”.
(1)求函数y=![]() x-3的图象上所有“湘一点”的坐标;
x-3的图象上所有“湘一点”的坐标;
(2)若直线y=mx+m(m为常数)与直线y=x-2的交点为“湘一点”,试求出整数m的值.
(3)若直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,试求出常数b的取值范围.
【答案】(1)函数y=![]() x-3的图象上“湘一点”的坐标是(0,-3);(2)m=0或m=2;(3)10<b≤12或-4≤b<-2
x-3的图象上“湘一点”的坐标是(0,-3);(2)m=0或m=2;(3)10<b≤12或-4≤b<-2
【解析】
(1)根据题意和湘一点的定义可以解答本题;
(2)将两个一次函数联立方程组,解方程组,再根据整点的条件分析讨论;
(3)画出图形,利用特殊点解决问题即可;
(1)∵x是整数,x≠0时,![]() x是一个无理数,
x是一个无理数,
∴x≠0时,![]() x-3不是整数,
x-3不是整数,
∴x=0,y=-3,
即函数y=![]() x-3的图象上“湘一点”的坐标是(0,-3);
x-3的图象上“湘一点”的坐标是(0,-3);
(2)解![]() ,得x=-1-
,得x=-1-![]() ,
,
∵交点为“湘一点”,且m为整数,
∴m=0或m=2,
(3)如图,当直线y=-x+b经过A(5,7)时,b=12,
当直线y=-x+b经过点B(4,6)时,b=10.
当直线y=-x+b经过点C(-2,0)时,b=-2.
当直线y=-x+b经过点D(-3,-1)时,b=-4.

观察图象可知:直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,常数b的取值范围10<b≤12或-4≤b<-2.

练习册系列答案
相关题目