题目内容
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
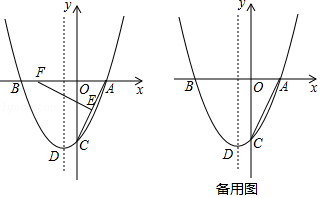
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 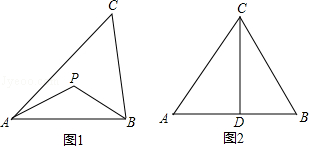
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
【答案】
(1)解:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= ![]() DB=
DB= ![]() AB,
AB,
与已知PD= ![]() AB矛盾,∴PB≠PC,
AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= ![]() AB,得PD=BD,
AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°
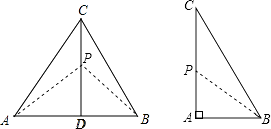
(2)解:∵BC=5,AB=3,
∴AC= ![]() =
= ![]() =4,
=4,
①若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x= ![]() ,即PA=
,即PA= ![]() ,
,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 ![]() .
.
【解析】应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数; 探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).

 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案【题目】某校在一次广播操比赛中,初二 (1)班、初二(2)班、初二(3)班的各项得分如下:
服装统一 | 动作整齐 | 动作准确 | |
初二(1)班 |
|
|
|
初二(2)班 |
|
|
|
初二(3)班 |
|
|
|
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是________;在动作整齐方面三个班得分的众数是________;在动作准确方面最有优势的是________班.
(2)如果服装统一、动作整齐、动作准确三个方面的重要性之比为![]() ,那么这三个班的排名顺序怎样?为什么?
,那么这三个班的排名顺序怎样?为什么?
(3)在(2)的条件下,你对三个班级中排名最靠后的班级有何建议?