��Ŀ����
����Ŀ��ijУΪ�˸��õؿ�չ�����˶��������������1600Ԫ��������8��������14������������ĵ��۱�����ĵ��۶�20Ԫ�������������⣺
��1��������������ĵ��ۣ�
��2����ѧУ���ò�����3240Ԫ���Ҳ�����3200Ԫ�ٴι���������50����������ļ��ֹ�����
��3���ڣ�2���������£�����֪����Ľ���Ϊ50Ԫ������Ľ���Ϊ65Ԫ�����ڵڶ��ι����У����ַ����̼һ�����ࣿ
���𰸡�
��1���⣺������ĵ���ΪxԪ��������ĵ���Ϊ��x+20��Ԫ��
�������⣬��8x+14��x+20��=1600��
��ã�x=60��x+20=80��
������ĵ���Ϊ60Ԫ��������ĵ���Ϊ80Ԫ��
��2���⣺�蹺������y����������50��y������
�������⣬�� ![]() ��
��
��ã� ![]() ��
��
��y������
��y=38��39��40��
��y=38��50��y=12��
��y=39��50��y=11��
��y=40��50��y=10��
�������ַ�����
����һ����������38����������12����
����������������39����������11����
����������������40����������10����
��3���⣺�̼��۷���һ������38��60��50��+12��80��65��=560��Ԫ����
�̼��۷�����������39��60��50��+11��80��65��=555��Ԫ����
�̼��۷�����������40��60��50��+10��80��65��=550��Ԫ����
�ʵڶ��ι����У�����һ�̼һ������
����������1��������ĵ���ΪxԪ��������ĵ���Ϊ��x+20��Ԫ�������������Ǯ��Ϊ1600Ԫ���ɵó����̣�������ɣ���2���������������IJ��ȹ�ϵ��������3240Ԫ���Ҳ�����3200Ԫ��������ϵ��������50�����ɵó�����ʽ�飬������ɣ���3���ֱ�������ַ��������̶��ȽϿɵó��𰸣�
�����㾫����������Ҫ������һԪһ�β���ʽ���Ӧ�õ����֪ʶ�㣬��Ҫ����1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸲�����ȷ�����⣮

 ��У����ϵ�д�
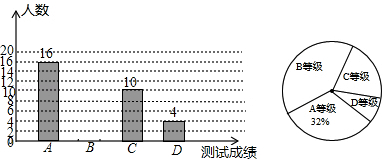
��У����ϵ�д�����Ŀ��ijУ��һ�ι㲥�ٱ����У����� ��1���ࡢ������2���ࡢ������3����ĸ���÷����£�
��װͳһ | �������� | ����ȷ | |
������1���� |
|
|
|
������2���� |
|
|
|
������3���� |
|
|
|
��1����գ����ݱ����ṩ����Ϣ���ڷ�װͳһ���棬������÷ֵ�ƽ������________���ڶ������뷽��������÷ֵ�������________���ڶ���ȷ�����������Ƶ���________�࣮
��2�������װͳһ���������롢����ȷ�����������Ҫ��֮��Ϊ![]() ����ô�������������˳��������Ϊʲô��
����ô�������������˳��������Ϊʲô��
��3���ڣ�2���������£���������༶���������İ༶�кν��飿