Question

【题目】如图，在等边△ABC中， BC＝8，以AB为直径的⊙O与边AC、BC分别交于点D、E，过点D作DF⊥BC，垂足为F．

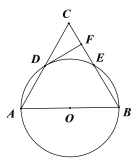
（1）求证：DF为⊙O的切线．

（2）求弧DE的长度．

（3）求EF的长．

Answer 1

【答案】（1）见解析；（2）；（3）2

【解析】

（1）连接DO，先证出△OAD是等边三角形，故∠ADO＝60°，再求出∠CDF，最后证出OD⊥DF，利用切线的判定即可得到.DF为⊙O的切线；

（2）连接OD、OE，先求出∠DOE的度数，再代入弧长公式即可；

（3）先求出CD的长，再求CF的长，利用EF=BC-CF-BE即可.

（1）证明：连接DO，

∵△ABC是等边三角形，

∴∠A＝∠C＝60°，

∵OA＝OD，

∴△OAD是等边三角形，

∴∠ADO＝60°，

∵DF⊥BC，

∴∠CDF＝90°﹣∠C＝30°，

∴∠FDO＝180°﹣∠ADO﹣∠CDF＝90°，

即OD⊥DF，

∵OD为半径，

∴DF为⊙O的切线；

（2）连接OD、OE

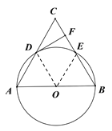
∵EO=OB，∠EOB=60°

∴△OBE是等边三角形，

∴∠EOB =60°

∴∠DOE=180°－∠EOB－AOD=60°

∵AB=BC=8

∴的半径为4

∴

（3）解：∵△OAD是等边三角形，

∴AD＝AO＝AB＝4，

∴CD＝AC﹣AD＝4，

Rt△CDF中，∠CDF＝30°，

∴CF＝CD＝2，DF＝2，

连接OE，

∵OB＝OE，∠B＝60°，

∴△OBE是等边三角形，

∴OB＝BE＝4，

∴EF＝BC﹣CF﹣BE＝8﹣2﹣4＝2；