题目内容
【题目】综合题。
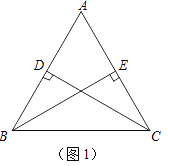
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
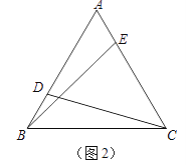
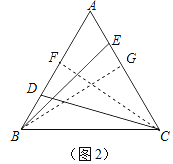
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
【答案】(1)证明见解析(2)CD=BE
【解析】试题分析:(1)利用AAS证明△ABE≌△ACD,利用全等三角形的性质即可证得结论;(2)分别作CF⊥AB,BG⊥AC,CD=BE,利用AAS证明△FBC≌△GCB,根据全等三角形的对应边相等可得CF=BG;再证得∠ADC=∠BEG,利用AAS证明△CFD≌△BGE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)证明:∵CD⊥AB于点D,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中, 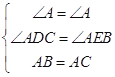 ,
,
∴△ABE≌△ACD(AAS).
∴CD=BE
(2)CD=BE, 证明如下:分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中, 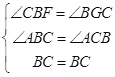 ,
,
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中, 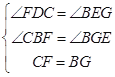 ,
,
∴△CFD≌△BGE,
∴CD=BE.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目