Question

【题目】二次函数＝＋＋的顶点Ｍ是直线＝－和直线＝＋的交点．

（1）若直线＝＋过点D（0，－3），求M点的坐标及二次函数＝＋＋的解析式；

（2）试证明无论取任何值，二次函数＝＋＋的图象与直线＝＋总有两个不同的交点；

（3）在（1）的条件下，若二次函数＝＋＋的图象与轴交于点C，与的右交点为A，试在直线＝－上求异于M的点P，使P在△CMA的外接圆上．

Answer 1

【答案】（1）M点坐标为M（2，－1），二次函数＝＋＋的解析式为： ＝－4＋3；

（2）证明见解析；

（3）P（－， ）

【解析】（本小题满分１４分）

解：（１）把Ｄ（０，－３）坐标代入直线＝＋中，

得＝－３，从而得直线＝－３．……………………………………………１分

由Ｍ为直线＝－与直线＝－３的交点，

得，………………………………………………………………………２分

解得，∴得Ｍ点坐标为Ｍ（２，－１）．…………………………………３分

∵Ｍ为二次函数＝＋＋的顶点，∴其对称轴为＝２，

由对称轴公式： ＝－，得－＝２，∴＝－４；

由＝－１，得＝－１，得＝３．

∴二次函数＝＋＋的解析式为： ＝－４＋３；………………４分

［也可用顶点式求得解析式：由Ｍ（２，－１），

得＝－１，展开得＝－４＋３］

（２）∵Ｍ是直线＝－和＝＋的交点，得，

解得，∴得Ｍ点坐标为Ｍ（－， ）．…………………………１分

从而有－＝－和＝，

解得＝； ＝＋．…………………………………………………３分

由，得＋（－１）＋－＝０，……………………４分

该一元二次方程根的判别式

⊿＝（－１）２－４（－）

＝（－１）２－４（＋－）＝１＞０，…………………………５分

∴二次函数＝＋＋的图象与直线＝＋总有两个不同的交点；

（３）解法①：

由（１）知，二次函数的解析式为： ＝－４＋３，

当＝０时， ＝３．∴点Ｃ的坐标为Ｃ（０，３）．……………………………１分

令＝０，即－４＋３＝０，解得＝１， ＝３，

∴点Ａ的坐标为Ａ（３，０）．………………………………………………………２分

由勾股定理，得ＡＣ＝３．∵Ｍ点的坐标为Ｍ（２，－１），

过Ｍ点作轴的垂线，垂足的坐标应为（２，０），由勾股定理，

得ＡＭ＝；过Ｍ点作轴的垂线，垂足的坐标应为（０，－１），

由勾股定理，得ＣＭ＝＝＝２．

∵ＡＣ２＋ＡＭ２＝２０＝ＣＭ２，∴△ＣＭＡ是直角三角形，……………………３分

ＣＭ为斜边，∠ＣＡＭ＝９０°．

直线＝－与△ＣＭＡ的外接圆的一个交点为Ｍ，另一个交点为Ｐ，

则∠ＣＰＭ＝９０°．即△ＣＰＭ为Ｒt△．………………………………………４分

设Ｐ点的横坐标为，则Ｐ（，－ ）．过点Ｐ作轴垂线，

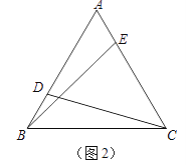
过点Ｍ作轴垂线，两条垂线交于点Ｅ（如图４），则Ｅ（，－１）．

过Ｐ作ＰＦ⊥轴于点Ｆ，则Ｆ（０，－ ）．

在Ｒt△ＰＥＭ中，ＰＭ２＝ＰＥ２＋ＥＭ２

＝（－＋１）２＋（２－）２＝－５＋５．

在Ｒt△ＰＣＦ中，ＰＣ２＝ＰＦ２＋ＣＦ２＝＋（３＋）２

＝＋３＋９．在Ｒt△ＰＣＭ中，ＰＣ２＋ＰＭ２＝ＣＭ２，

得＋３＋９＋－５＋５＝２０，

化简整理得５－４－１２＝０，解得＝２， ＝－．

当＝２时， ＝－１，即为Ｍ点的横、纵坐标．

∴P点的横坐标为－，纵坐标为．

∴Ｐ（－， ）．……………………………………………………………………５分

解法②［运用现行高中基本知识（解析几何）：线段中点公式及两点间距离公式］：

设线段ＣＭ的中点（即△ＣＭＡ内接圆的圆心）为Ｈ，则由线段中点公式，可求出Ｈ的坐标为Ｈ（１，１）．∵点Ｐ在⊙Ｈ上，∴点Ｐ到圆心Ｈ的距离等于半径．

设点Ｐ的坐标为：Ｐ（，－ ），由两点间的距离公式，得ＰＨ的长度为：

，从而有： ＝，即

＝５，化简，整理，得化简整理得５－４－１２＝０，解得＝２， ＝－．当＝２时， ＝－１，即为Ｍ点的横、纵坐标．

∴P点的横坐标为－，纵坐标为．

∴Ｐ（－， ）．