题目内容
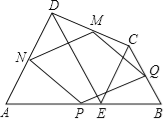
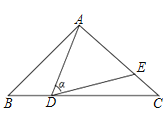
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cos∠α=![]() ,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
,下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
;④0<CE≤6.4.其中正确的结论是_________.(把你认为正确结论的序号都填上)
【答案】①②④
【解析】
①根据有两组对应角相等的三角形相似即可证明;②由BD=6,则DC=10,然后根据有两组对应角相等且夹边也相等的三角形全等,即可证得;③分两种情况讨论,通过三角形相似即可求得;④依据相似三角形对应边成比例即可求得.
解:①∵AB=AC,
∴∠B=∠C,
又∵∠ADE=∠B,
∴∠ADE=∠C,
∴△ADE∽△ACD,故①正确;
②作AG⊥BC于G,

∵AB=AC=10,∠ADE=∠B=α,cosα=![]() ,
,
∴BG=ABcosB,
∴BC=2BG=2ABcosB=2×10×![]() =16,
=16,
∵BD=6,
∴DC=10,
∴AB=DC,
在△ABD与△DCE中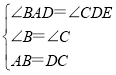 ,
,
∴△ABD≌△DCE(ASA),故②正确;
③当∠AED=90°时,由①可知:△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,
∴∠ADC=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
∴∠ADE=∠B=α且cosα=![]() ,AB=10,BD=8,
,AB=10,BD=8,
当∠CDE=90°时,易△CDE∽△BAD,
∵∠CDE=90°,
∴∠BAD=90°,
∵∠B=α且cosα=![]() ,AB=10,
,AB=10,
∴cosB=![]() =
=![]() ,
,
∴BD=![]() ,故③错误;
,故③错误;
④易证得△CDE∽△BAD,由②可知BC=16,
设BD=y,CE=x,
∴![]() ,
,
∴![]() ,
,
整理得:y216y+64=6410x,
即(y8)2=6410x,
∴0<x≤6.4,故④正确;
故答案为:①②④.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
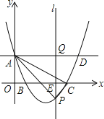
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
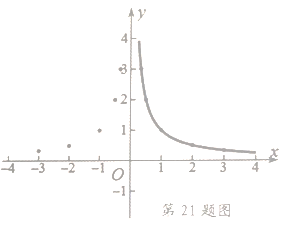
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.