题目内容
【题目】如图，在四边形ABCD中，E是AB上的一点，△ADE和△BCE都是等边三角形，点P、Q、M、N分别为AB、BC、CD、DA的中点，则四边形MNPQ是（ ）
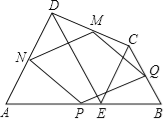
A.等腰梯形B.矩形C.菱形D.正方形
【答案】C
【解析】
试题连接AC与BD，首先证得△AEC≌△DEB，即可得到AC=BD，然后利用三角形的中位线定理证得四边形MNPQ的对边平行且相等，并且邻边相等，从而证得四边形MNPQ是菱形．
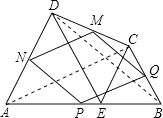
证明：连接BD、AC；
∵△ADE、△ECB是等边三角形，
∴AE=DE，EC=BE，∠AED=∠BEC=60°；
∴∠AEC=∠DEB=120°；
在△AEC与△DEB中，
，
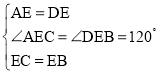∴△AEC≌△DEB（SAS）；
∴AC=BD；
∵M、N是CD、AD的中点，
∴MN是△ACD的中位线，即MN=
AC，
同理可证得：NP=DB，QP=AC，MQ=BD，
∴MN=NP=PQ=MQ，
∴四边形NPQM是菱形．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
