ЬтФПФкШн
ЁОЬтФПЁПаЁЖЋЭЌбЇИљОнКЏЪ§ЕФбЇЯАОбщЃЌЖдКЏЪ§y ![]()
![]() НјааСЫЬНОПЃЌЯТУцЪЧЫћЕФЬНОПЙ§ГЬЃК
НјааСЫЬНОПЃЌЯТУцЪЧЫћЕФЬНОПЙ§ГЬЃК
ЃЈ1ЃЉвбжЊxЃНЃ3ЪБ![]() 0ЃЛxЃН1 ЪБ
0ЃЛxЃН1 ЪБ![]() 0ЃЌЛЏМђЃК
0ЃЌЛЏМђЃК
ЂйЕБxЃМЃ3ЪБЃЌyЃН
ЂкЕБЃ3ЁмxЁм1ЪБЃЌyЃН
ЂлЕБxЃО1ЪБЃЌyЃН
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЛГіy ![]()
![]() ЕФЭМЯёЃЌИљОнЭМЯёЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪ.
ЕФЭМЯёЃЌИљОнЭМЯёЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪ.
ЃЈ3ЃЉИљОнЩЯУцЕФЬНОПНтОіЃЌЯТУцЮЪЬтЃК
вбжЊA(a,0)ЪЧxжсЩЯвЛЖЏЕуЃЌB(1,0)ЃЌC(Ѓ3,0)ЃЌдђABЃЋACЕФзюаЁжЕЪЧ

ЁОД№АИЁПЃЈ1ЃЉЂй-2-2xЃЛЂк4ЃЛЂл2x+2ЃЛЃЈ2ЃЉЭМЯѓМћНтЮіЃЌКЏЪ§ЭМЯѓВЛЙ§дЕуЃЛЃЈ3ЃЉ4
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўМАОјЖджЕЕФЛЏМђЗЈдђМЦЫуМДПЩЃЛ
ЃЈ2ЃЉЛГіКЏЪ§ЭМЯѓЃЌдђвзЕУвЛЬѕКЏЪ§аджЪЃЛ
ЃЈ3ЃЉAЃЈaЃЌ0ЃЉЮЛгкЕуBЃЈ1ЃЌ0ЃЉКЭЕуCЃЈ-3ЃЌ0ЃЉжЎМфЪБЃЌAB+ACЕШгкЯпЖЮBCЕФГЄЃЌДЫЪБЮЊЦфзюаЁжЕЃЎ
ЃЈ1ЃЉЁпx=-3ЪБ|x+3|=0ЃЛx=1ЪБ|x-1|=0
ЁрЂйЕБxЃМ-3ЪБЃЌy=1-x-x-3=-2-2xЃЛ
ЂкЕБ-3ЁмxЁм1ЪБЃЌy=1-x+x+3=4ЃЛ
ЂлЕБxЃО1ЪБЃЌy=x-1+x+3=2x+2ЃЛ
ЙЪД№АИЮЊЃК-2-2xЃЛ4ЃЛ2x+2ЃЎ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЛГіy=|x-1|+|x+3|ЕФЭМЯѓЃЌШчЭМЫљЪОЃК
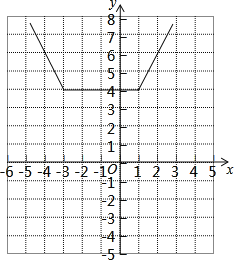
ИљОнЭМЯѓЃЌИУКЏЪ§ЭМЯѓВЛЙ§дЕуЃЎ
ЙЪД№АИЮЊЃККЏЪ§ЭМЯѓВЛЙ§дЕуЃЛ
ЃЈ3ЃЉИљОнЩЯУцЕФЬНОППЩжЊЕБAЃЈaЃЌ0ЃЉЮЛгкЕуBЃЈ1ЃЌ0ЃЉКЭЕуCЃЈ-3ЃЌ0ЃЉжЎМфЪБЃЌAB+ACгазюаЁжЕ4ЃЎ
ЙЪД№АИЮЊЃК4ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ