题目内容
【题目】综合与探究
如图，在平面直角坐标系中，
，点
．
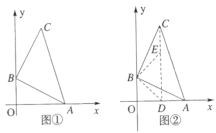
（1）在图①中，点
坐标为__________；
（2）如图②，点
在线段
上，连接
，作等腰直角三角形
，
，连接
．证明：
；
（3）在图②的条件下，若
三点共线，求
的长；
（4）在
轴上找一点
，使
面积为2．请直接写出所有满足条件的点的坐标．
【答案】(1)(1,3)；
(2)答案见解析；
(3)OD=1
(4)F的坐标是
或
【解析】
（1）过C点作
轴，垂足为F，在证明了
后可得到线段BM、CM的长，再求出线段OM的长，便可得点C的坐标；
(2)根据
和等式的基本性质证明
,再利用“SAS”定理证明
后便可得到
；
(3) 
三点共线时，可推导出
轴，从而有
；
(4)根据点F在y轴上，所以
中BF上的高总是OA=2，在此处只需要利用其面积为2和三角形的面积计算：
，分点F在点B的上方和下方两种情况讨论可得．
(1)过点C作轴，垂足为M，则
∴
∵
∴
∴
又∵
∴
∴
， 
∵点
∴
， 
∴
而点C在第一象限，所以点
(2)∵
等腰直角三角形
∴
∵
∴
∴
∴
∴
(3)由(2) 可得
∵三点共线且三角形
是等腰直角三角形
∴
∴
又
∴四边形ODCM是矩形
∴
(4)∵点F在y轴上
∴的边BF的高为OA=2
∵
即
∴
当点F在点B的上方时，其坐标为(3,0)；
当点F在点B的下方时，其坐标为(-1,0)．
故点F的坐标为(3,0)或(-1,0)．
练习册系列答案
相关题目
