题目内容
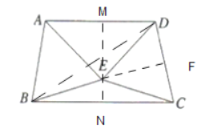
【题目】如图，
与
是两个全等的等边三角形，
，下列结论不正确的是（ ）
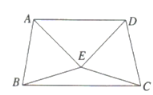
A.
B.直线
垂直平分
C.
D.四边形
是轴对称图形
【答案】A
【解析】
根据
与
是两个全等的等边三角形，可得到
，
，
，然后结合
，先计算出
的大小，便可计算出的大小，从而判定出AD与BC的位置关系及BE与DC的关系，同时也由于
与
是等腰三角形，也容易确定四边形ABCD的对称性．
（1）∵与是两个全等的等边三角形
∴，， 
∴
∵
∴
∴
，
∴
，所以选项A错误；
（2）由（1）得：
∴
∴
，所以选项C正确；
（3）延长BE交CD于点F，连接BD．
∵
，
∴
∴
∴
即
在
与
中
∴
∴
∴
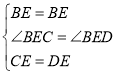
，综上，BE垂直平分CD,所以答案B正确；
（4）过E作
，由得
而
和
是等腰三角形，则MN垂直平分AD、BC，所以四边形ABCD是軕对称图形，所以选项Ｂ正确．
故选：Ａ
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
