题目内容
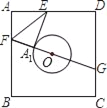
【题目】如图,已知正方形纸片ABCD的边是⊙O半径的4倍,点O是正方形ABCD的中心,将纸片保持图示方式折叠,使EA1恰好与⊙O相切于点A1,则tan∠A1EF的值为_____.
【答案】![]()
【解析】
在Rt△FMO中利用勾股定理得出AF与r的关系,设r=6a,则x=7a,AM=MO=12a,FM=5a,AF=FA1=7a,利用A1N∥OM得到![]() 求出AN,NA1,再证明∠1=∠2即可解决问题.
求出AN,NA1,再证明∠1=∠2即可解决问题.
如图,连接AA1,EO,作OM⊥AB,A1N⊥AB,垂足分别为M、N.
设⊙O的半径为r,则AM=MO=2r,设AF=FA1=x,
在Rt△FMO中,∵FO2=FM2+MO2,
∴(r+x)2=(2r﹣x)2+(2r)2,
∴7r=6x,
设r=6a则x=7a,AM=MO=12a,FM=5a,AF=FA1=7a,
∵A1N∥OM,
∴![]() ,
,
∴![]() ,
,
∴A1N=![]() a,FN=
a,FN=![]() a,AN=
a,AN=![]() a,
a,
∵∠1+∠4=90°,∠4+∠3=90°,∠2=∠3,
∴∠1=∠3=∠2,
∴tan∠2=tan∠1=![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目