��Ŀ����
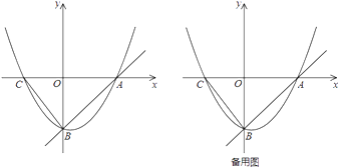
����Ŀ��ƽ��ֱ������ϵxOy�У�������Ϊa�ĵ�A�ڷ���������y1��![]() (x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(x��0)��ͼ���ϣ���A���A���ڵ�O�Գƣ�һ�κ���y2��mx+n��ͼ����A��
(1)��a��2����B(4��2)�ں���y1��y2��ͼ���ϣ�
���ֱ�����y1��y2�ı���ʽ��
��ֱ��д��ʹy1��y2��0������x�ķ�Χ��
(2)��ͼ���躯��y1��y2��ͼ���ཻ�ڵ�B����B�ĺ�����Ϊ3a����AA��B�����Ϊ16����k��ֵ��
���𰸡�(1)��![]() , y2=x��2;��2<x<4��(2)6.
, y2=x��2;��2<x<4��(2)6.
��������
��1������֪��������꼴����
��2������������ת��Ϊ��AOB������ٸ���S��AOB��S�ı���ACDB���⼴�ɵý���
��1��������֪����B��4��2����y1�T![]() ��x��0����ͼ��������k��8����y1
��x��0����ͼ��������k��8����y1![]() ��
��
��a��2�����A������2��4����A����������2����4����
��B��4��2����A����2����4������y2��mx+n������![]() �������
�������![]() ����y2��x��2��
����y2��x��2��
����y1��y2��0ʱ��y1![]() ͼ����y2��x��2ͼ���Ϸ�����������ͼ����x���Ϸ�������ͼ�����2��x��4��
ͼ����y2��x��2ͼ���Ϸ�����������ͼ����x���Ϸ�������ͼ�����2��x��4��
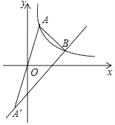
��2���ֱ����A��B��AC��x���ڵ�C��BD��x���ڵ�D����BO��

��OΪAA���е���S��AOB![]() S��ABA����8��
S��ABA����8��
�ߵ�A��B��˫����������S��AOC��S��BOD����S��AOB��S�ı���ACDB��8��
����֪��A��B���궼��ʾΪ��a��![]() ����3a��
����3a��![]() ������
������![]() ��
��
�����k��6��