题目内容
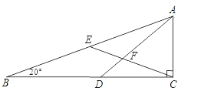
【题目】如图,△ABC中,∠C=90°,D在CB上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE=( )
A. 40° B. 50° C. 60° D. 70°
【答案】C
【解析】
已知AD=DB,∠B=20°,由等腰三角形的性质可得∠B=∠BAD =20°,根据三角形外角的性质可得∠ADC=∠B+∠BAD =40°,又因∠C=90°,E为AB的中点,根据直角三角形斜边的中线等于斜边的一半可得AE=BE=EC,所以∠BCE=∠B=20°,再根据三角形外角的性质可得 ∠DFE=∠BC E+∠ADC =20°+40°=60°.
∵AD=DB,∠B=20°,
∴∠B=∠BAD =20°,
∴∠ADC=∠B+∠BAD =40°,
∵∠C=90°,E为AB的中点,
∴AE=BE=EC,
∴∠BCE=∠B=20°,
∴∠DFE=∠BC E+∠ADC =20°+40°=60°.
故选C.

练习册系列答案
相关题目