Question

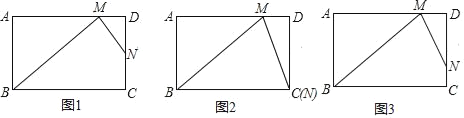
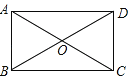
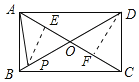
【题目】已知：如图，矩形ABCD，AB＝2，BC＝4，对角线AC，BD相交于点O，点P在对角线BD上，并且A，O，P组成以OP为腰的等腰三角形，那么OP的长等于___．

Answer 1

【答案】或.

【解析】

由矩形的性质和勾股定理得出OA＝OB＝OC＝OD＝，当P与B或D重合时，OP＝OB＝OD＝；当AP＝OP时，作PE⊥OA于E，作DF⊥AC于F，则OE＝OA＝， PE∥DF，得出△OPE∽△ODF，得出＝，求出OF＝，

代入比例式得出OP＝即可．

∵四边形ABCD是矩形，

∴AD＝BC＝4，CD＝AB＝2，∠ABC＝90°，OA＝OC，OB＝OD，AC＝BD，

∴AC＝ ，

∴OA＝OB＝OC＝OD＝，

当P与B或D重合时，OP＝OB＝OD＝；

当AP＝OP时，作PE⊥OA于E，作DF⊥AC于F，如图所示：

则OE＝OA＝，PE∥DF，

∴△OPE∽△ODF，

∴＝，

∵△ADC的面积＝AD×CD＝AC×DF，

∴DF＝ ，

∴OF＝ ，

∴ ，

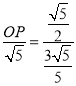解得：OP＝ ；

综上所述，A，O，P组成以OP为腰的等腰三角形，那么OP的长等于或；

故答案为：或．