题目内容
【题目】如图所示，某海盗船以20海里/小时的速度在某海域执行巡航任务，当海监船由西向东航行至A处使，测得岛屿P恰好在其正北方向，继续向东航行1小时到达B处，测得岛屿P在其北偏西30°方向，保持航向不变又航行2小时到达C处，求出此时海监船与岛屿P之间的距离（即PC的长，结果精确到0.1）（参考数据：
≈1.732，
≈1.414）
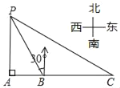
【答案】PC≈69.3（海里）．
【解析】
首先证明PB=BC，推出∠C=30°，可得PC=2PA，求出PA即可解决问题．
在Rt△PAB中，∵∠APB＝30°，
∴PB＝2AB，
由题意BC＝2AB，
∴PB＝BC，
∴∠C＝∠CPB，
∵∠ABP＝∠C+∠CPB＝60°，
∴∠C＝30°，
∴PC＝2PA，
∵PA＝ABtan60°，
∴PC＝2×20×
≈69.3（海里）．
练习册系列答案
相关题目
