题目内容
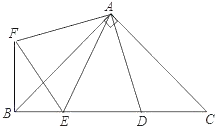
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
【答案】(1)见解析;(2)EF=![]() .
.
【解析】
(1)由旋转的性质可求∠FAE=∠DAE=45°,即可证△AEF≌△AED,可得EF=ED;
(2)由旋转的性质可证∠FBE=90°,利用勾股定理和方程的思想可求EF的长.
(1)∵∠BAC=90°,∠EAD=45°,
∴∠BAE+∠DAC=45°,
∵将△ADC绕点A顺时针旋转90°,得到△AFB,
∴∠BAF=∠DAC,AF=AD,CD=BF,∠ABF=∠ACD=45°,
∴∠BAF+∠BAE=45°=∠FAE,
∴∠FAE=∠DAE,AD=AF,AE=AE,
∴△AEF≌△AED(SAS),
∴DE=EF
(2)∵AB=AC=2![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=4,
∵CD=1,
∴BF=1,BD=3,即BE+DE=3,
∵∠ABF=∠ABC=45°,
∴∠EBF=90°,
∴BF2+BE2=EF2,
∴1+(3﹣EF)2=EF2,
∴EF=![]()

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】公司有345台电脑需要一次性运送到某学校,计划租用甲、乙两种货车共8辆已知每辆甲种货车一次最多运送电脑45台、租车费用为400元,每辆乙种货车一次最多运送电脑30台、租车费用为280元
(Ⅰ)设租用甲种货车![]() 辆(
辆(![]() 为非负整数),试填写下表.
为非负整数),试填写下表.
表一:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用的甲种货车最多运送电脑的数量/台 | 135 | ||
租用的乙种货车最多运送电脑的数量/台 | 150 |
表二:
租用甲种货车的数量/辆 | 3 | 7 |
|
租用甲种货车的费用/元 | 2800 | ||
租用乙种货车的费用/元 | 280 |
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由