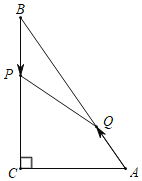
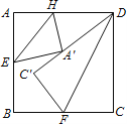
题目内容
【题目】如图,正方形ABCD的边长为6,点E,F分别为AB、BC的中点,点H是AD边上一点,将△DCF沿DF折叠得△DC′F,将△AEH沿EH折叠后点A的对应点A′刚好落在DC′上,则cos∠DA′H=______.
【答案】![]() .
.
【解析】
延长DC'交AB于K,连接FK,分别过H,E作DK的垂线,垂足分别为M,N,利用正方形的性质及轴对称的性质,先证Rt△FBK≌Rt△FC'K,推出BK=C'K,在Rt△ADK中,利用勾股定理求出BK,C'K的长,进一步求出EK的长,在Rt△KEN与Rt△KAD中,利用三角函数求出EN的长,在Rt△EA'N中,求出cos∠A'EN的值,证∠DA'H与∠A'EN相等即可.
解:如图,延长DC'交AB于K,连接FK,分别过H,E作DK的垂线,垂足分别为M,N,
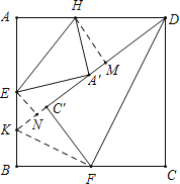
∵四边形ABCD为正方形,
∴∠A=∠∠B=∠C=90°,AB=BC=6,
∵E,F分别为AB,BC的中点,
∴AE=BE=BF=FC=![]() ×6=3,
×6=3,
由翻折知,△DCF≌△DC'F,△AEH≌△A'EH,
∴∠FC'D=∠C=90°,∠A=∠HA'E=90°,AE=A'E=3,C'F=CF=BF=3,DC'=DC=6,
∴∠B=∠FC'K=90°,
又∵KF=KF,
∴Rt△FBK≌Rt△FC'K(HL),
∴KB=KC',
设KB=KC'=x,
在Rt△ADK中,AD=6,AK=6-x,DK=6+x,
∵DK2=AD2+AK2,
∴(6+x)2=62+(6-x)2,
解得:x=![]() ,
,
∴BK=C'K=![]() ,
,
∴DK=DC'+KC'=6+![]() =
=![]() ,EK=BE-BK=
,EK=BE-BK=![]() ,
,
在Rt△KNE与Rt△KAD中,
sin∠EKN=![]() ,
,
即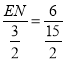 ,
,
解得,EN=![]() ,
,
∵∠DA'H+∠EA'N=90°,∠EA'N+∠NEA'=90°,
∴∠HA'D=∠NEA',
在Rt△EA'N中,cos∠A'EN=![]() =
=![]() =
=![]() ,
,
即cos∠DA'H=![]() ,
,
故答案为:![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的![]() 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下
将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下![]() 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数n | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数m | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 |
|
|
|
|
|
|
|
|
|
|
下面有三个推断:![]() 投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是
投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是![]() ;
;![]() 随着实验次数的增加,“兵”字面朝上的频率总在
随着实验次数的增加,“兵”字面朝上的频率总在![]() 附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是
附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是![]() ;
;![]() 当实验次数为200次时,“兵”字面朝上的频率一定是
当实验次数为200次时,“兵”字面朝上的频率一定是![]() 其中合理的是
其中合理的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()