题目内容
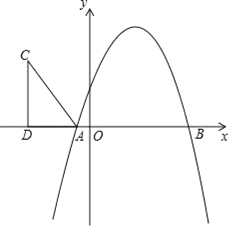
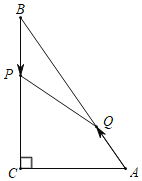
【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm.点P从B出发,沿BC方向,以1cm/s的速度向点C运动,点Q从A出发,沿AB方向,以2cm/s的速度向点B运动;若两点同时出发,当其中一点到达端点时,两点同时停止运动,设运动时间为t(s)(t>0),△BPQ的面积为S(cm2).
(1)t=2秒时,则点P到AB的距离是 cm,S= cm2;
(2)t为何值时,PQ⊥AB;
(3)t为何值时,△BPQ是以BP为底边的等腰三角形;
(4)求S与t之间的函数关系式,并求S的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)S=﹣
;(4)S=﹣![]() t2+3t,S的最大值为
t2+3t,S的最大值为![]() .
.
【解析】
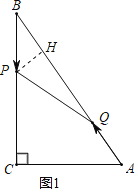
(1)作PH⊥AB于H,根据勾股定理求出AB,证明△BHP∽△BCA,根据相似三角形的性质列出比例式,求出PH,根据三角形的面积公式求出S;
(2)根据△BQP∽△BCA,得到![]() =
=![]() ,代入计算求出t即可;
,代入计算求出t即可;
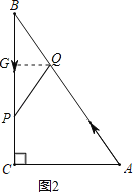
(3)过Q作QG⊥BC于G,证明△QBG∽△ABC,根据相似三角形的性质列式计算,得到答案;
(4)根据△QBG∽△ABC,用t表示出QG,根据三角形的面积公式列出二次函数关系式,根据二次函数的性质计算即可.
解:在Rt△ABC中,AC=6cm,BC=8cm,
由勾股定理得,AB=![]() =
=![]() =10cm,
=10cm,
∴0<t≤5,经过ts时,BP=t,AQ=2t,则BQ=10﹣2t,
(1)如图1,作PH⊥AB于H,
当t=2时,BP=2,BQ=10﹣2t=6,
∵∠BHP=∠BCA=90°,∠B=∠B,
∴△BHP∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:PH=![]() ,
,
∴S=![]() ×6×
×6×![]() =
=![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)当PQ⊥AB时,∠BQP=∠BCA=90°,∠B=∠B,
∴△BQP∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
则当t=![]() 时,PQ⊥AB;
时,PQ⊥AB;
(3)如图2,过Q作QG⊥BC于G,
∵QB=QP,QG⊥BC,
∴BG=GP=![]() t,
t,
∵∠BGQ=∠C=90°,∠B=∠B,
∴△QBG∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
∴当t=![]() 时,△BPQ是以BP为底边的等腰三角形;
时,△BPQ是以BP为底边的等腰三角形;
(4)由(3)可知,△QBG∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,QG=﹣![]() t+6,
t+6,
∴S=![]() ×t×(﹣
×t×(﹣![]() t+6),
t+6),
=﹣![]() t2+3t,
t2+3t,
=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
则当t=![]() 时,S的值最大,最大值为
时,S的值最大,最大值为![]() .
.

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】近日,某中学举办了一次以“弘扬传统文化”为主题的汉字听写比赛,初一和初二两个年级各有600名学生参加,为了更好地了解本次比赛成绩的分布情况,学校分别从两个年级随机抽取了若干名学生的成绩作为样本进行分析,下面是初二年级学生成绩样本的频数分布表和频数分布直方图(不完整,每组分数段中的分数包括最低分,不包括最高分)
初二学生样本成绩频数分布表 | ||
分组/分 | 频数 | 频率 |
50~60 | 2 | |
60~70 | 4 | 0.10 |
70~80 | 0.20 | |
80~90 | 14 | 0.35 |
90~100 | ||
合计 | 40 | 1.00 |
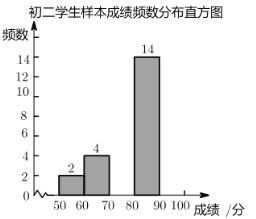
请根据所给信息,解答下列问题:
(1)补全成绩频数分布表和频数分布直方图.
(2)若初二学生成绩样本中80~90分段的具体成绩为:
80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
①根据上述信息,估计初二学生成绩的中位数为__________.
②若初一学生样本成绩的中位数为80,甲同学在比赛中得到了82分,在他所在的年级中位居275名,根据上述信息推断甲同学所在年级为__________(选填“初一”或者“初二”).
③若成绩在85分及以上均为“优秀”,请你根据抽取的样本数据,估计初二年级学生中达到“优秀”的学生人数为__________人.