题目内容
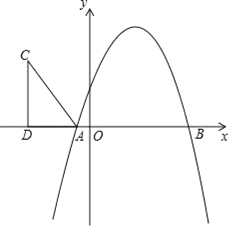
【题目】已知抛物线y=![]() x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D为第四象限抛物线上一点,设点D的横坐标为m,四边形ABCD的面积为S,求S与m的函数关系式,并求S的最值;
(3)点P在抛物线的对称轴上,且∠BPC=45°,请直接写出点P的坐标.

【答案】(1)y=![]() x2﹣x﹣4;(2)S=﹣(m﹣2)2+16,S的最大值为16;(3)点P的坐标为:(1,﹣1+
x2﹣x﹣4;(2)S=﹣(m﹣2)2+16,S的最大值为16;(3)点P的坐标为:(1,﹣1+![]() )或(1,﹣1﹣
)或(1,﹣1﹣![]() ).
).
【解析】
(1)根据交点式可求出抛物线的解析式;
(2)由S=S△OBC+S△OCD+S△ODA,即可求解;
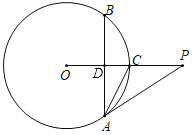
(3)∠BPC=45°,则BC对应的圆心角为90°,可作△BCP的外接圆R,则∠BRC=90°,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,证明△BMR≌△RNC(AAS)可求出点R(1,-1),即点R在函数对称轴上,即可求解.
解:(1)∵抛物线y=![]() x2+bx+c与x轴交于A(4,0)、B(﹣2,0),
x2+bx+c与x轴交于A(4,0)、B(﹣2,0),
∴抛物线的表达式为:y=![]() (x﹣4)(x+2)=
(x﹣4)(x+2)=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)设点D(m,![]() m2﹣m﹣4),可求点C坐标为(0,-4),
m2﹣m﹣4),可求点C坐标为(0,-4),
∴S=S△OBC+S△OCD+S△ODA
=![]()
![]()
=﹣(m﹣2)2+16,
当m=2时,S有最大值为16;
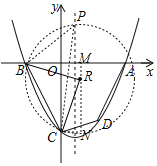
(3)∠BPC=45°,则BC对应的圆心角为90°,如图作圆R,则∠BRC=90°,
圆R交函数对称轴为点P,过点R作y轴的平行线交过点C与x轴的平行线于点N、交x轴于点M,设点R(m,n).
∵∠BMR+∠MRB=90°,∠MRB+∠CRN=90°,
∴∠CRN=∠MBR,
∠BMR=∠RNC=90°,BR=RC,
∴△BMR≌△RNC(AAS),
∴CN=RM,RN=BM,
即m+2=n+4,﹣n=m,
解得:m=1,n=﹣1,
即点R(1,﹣1),即点R在函数对称轴上,
圆的半径为:![]() =
=![]() ,
,
则点P的坐标为:(1,﹣1+![]() )或(1,﹣1﹣
)或(1,﹣1﹣![]() ).
).

【题目】近日,某中学举办了一次以“弘扬传统文化”为主题的汉字听写比赛,初一和初二两个年级各有600名学生参加,为了更好地了解本次比赛成绩的分布情况,学校分别从两个年级随机抽取了若干名学生的成绩作为样本进行分析,下面是初二年级学生成绩样本的频数分布表和频数分布直方图(不完整,每组分数段中的分数包括最低分,不包括最高分)
初二学生样本成绩频数分布表 | ||
分组/分 | 频数 | 频率 |
50~60 | 2 | |
60~70 | 4 | 0.10 |
70~80 | 0.20 | |
80~90 | 14 | 0.35 |
90~100 | ||
合计 | 40 | 1.00 |
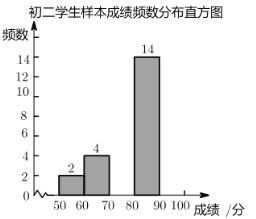
请根据所给信息,解答下列问题:
(1)补全成绩频数分布表和频数分布直方图.
(2)若初二学生成绩样本中80~90分段的具体成绩为:
80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
①根据上述信息,估计初二学生成绩的中位数为__________.
②若初一学生样本成绩的中位数为80,甲同学在比赛中得到了82分,在他所在的年级中位居275名,根据上述信息推断甲同学所在年级为__________(选填“初一”或者“初二”).
③若成绩在85分及以上均为“优秀”,请你根据抽取的样本数据,估计初二年级学生中达到“优秀”的学生人数为__________人.