题目内容
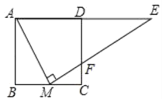
【题目】如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交CD于点F，交AD的延长线于点E，若AB＝4，BM＝2，则△DEF的面积为（ ）
A.9B.8C.15D.14.5
【答案】A
【解析】
由勾股定理可求AM的长，通过证明△ABM∽△EMA，可求AE=10，可得DE=6，由平行线分线段成比例可求DF的长，即可求解．
解：∵AB＝4，BM＝2，
∴
，
∵四边形ABCD是正方形，
∴AD∥BC，∠B＝∠C＝90°，
∴∠EAM＝∠AMB，且∠B＝∠AME＝90°，
∴△ABM∽△EMA，
∴
∴
∴AE＝10，
∴DE＝AE﹣AD＝6，
∵AD∥BC，即DE∥MC，
∴△DEF∽△CMF，
∴
，
∴
＝3，
∵DF+CF＝4，
∴DF＝3，
∴S△DEF＝
DE×DF＝9，
故选：A．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
