题目内容
【题目】如图,E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.

【答案】(1)见解析;(2) 24
【解析】
(1) 根据四边形ABCD是平行四边形,得到∠DAE=∠F,∠D=∠ECF,再根据E是平行四边形ABCD的边CD的中点,便可以证明出全等了.
(2) 由全等的性质,便可得到AE=EF=3,计算出DE的长度,最后计算CD即可.
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAE=∠F,∠D=∠ECF,
∵E是平行四边形ABCD的边CD的中点,∴DE=CE,
在△ADE和△FCE中,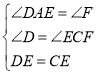 ,∴△ADE≌△FCE(AAS);
,∴△ADE≌△FCE(AAS);
(2)解:∵ADE≌△FCE,∴AE=EF=3,∵AB∥CD,∴∠AED=∠BAF=90°,
在平行四边形ABCD中,AD=BC=5,∴DE=![]() =4,∴CD=2DE=8.
=4,∴CD=2DE=8.
∴平行四边形ABCD的面积是:8×3=24.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)