题目内容
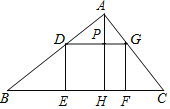
【题目】如图，矩形DEFG的边EF在△ABC的边BC上，顶点D，G分别在边AB，AC上，AH⊥BC，垂足为H，AH交DG于点P，已知BC＝6，AH＝4．当矩形DEFG面积最大时，HP的长是（ ）
A.1B.2C.3D.4
【答案】B
【解析】
首先设
，将AP用含x的代数式表示出来，运用矩形的性质、相似三角形的判定与性质表示出DG，根据矩形DEFG的面积S＝DG×DE，得到二次函数，用配方法求出函数的最大值．
解：设HP＝x，则DE＝GF＝x，
∵四边形DEFG是矩形，
∴DG＝EF，DE＝GF＝HP＝x，DG∥EF，
∵AH⊥BC，
∴AH⊥DG，
∵DG∥EF，
∴△ADG∽△ABC，
∴
，
∴
，
解得：DG＝
，
∴矩形DEFG的面积S＝DG×DE＝
x＝-
（x-2）2+6，
∵-＜0，
∴S有最大值，当x＝2时，S的最大值是6，
即当HP＝2时，矩形DEFG的面积最大，
故选：B．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
【题目】公司以10元/千克的价格收购一批产品进行销售，经过市场调查获悉，日销售量y（千克）是销售价格x（元/千克）的一次函数，部分数据如表：
销售价格x（元/千克） | 10 | 15 | 20 | 25 | 30 |
日销售量y（千克） | 300 | 225 | 150 | 75 | 0 |
（1）直接写出y与x之间的函数表达式；
（2）求日销售利润为150元时的销售价格；
（3）若公司每销售1千克产品需另行支出a元（0＜a＜10）的费用，当20≤x≤25时，公司的日获利润的最大值为1215元，求a的值．
