题目内容
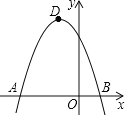
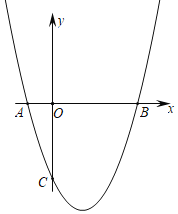
【题目】在平面直角坐标系中,点![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,
,
(1)若![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,当
上,当![]() 是边长为5的等腰三角形,共有几个这样的点
是边长为5的等腰三角形,共有几个这样的点![]() ,并尝试求出点
,并尝试求出点![]() 的坐标;
的坐标;
(2)若直线![]() 与
与![]() 不平行,
不平行,![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得
,使得![]() 是直角三角形,且
是直角三角形,且![]() ,若存在,求出这样的点
,若存在,求出这样的点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
【答案】(1) P1(3,4),P2(2,4),P3(8,4);(2) P1(1,3),P2(8,-4).
【解析】
(1)根据题意分PD=OD时,和 OP=OD,设P(x,4)根据两点之间的距离公式即可求解;
(2)如图,设出点P的坐标,过点P作PH⊥OC于点H,由△OPH∽△PCH得到![]() 建立方程求解.
建立方程求解.
(1)∵点![]() 是线段
是线段![]() 的中点,
的中点,![]()
∴D(5,0)
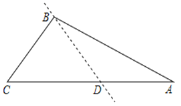
如图,①当PO=OD=5时,设P(x,4)
∴25=x2+42
解得x=3(-3舍去)
∴P1(3,4)
②当PD=OD=5时,设P(x,4)
∴25=(x-5)2+42
解得x1=2,x2=8
∴P2(2,4),P3(8,4)
∴点![]() 的坐标是P1(3,4),P2(2,4),P3(8,4);
的坐标是P1(3,4),P2(2,4),P3(8,4);
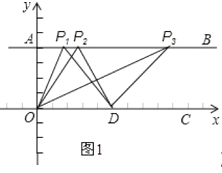
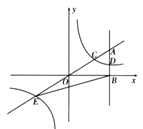
(2)设点P的坐标为(a,a+4),过点P作PH⊥OC于点H,
∵∠OPC=90°,![]() ,
,
∴△OPH∽△PCH.
∴![]() 即PH2=OH×CH.
即PH2=OH×CH.
∴(a+4)2=a(10a),
∴a28a+16=10aa2,
∴2a218a+16=0,解得a1=1,a2=8.
∴P1(1,3),P2(8,4).
即存在点P(1,3)或(8,4).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目