题目内容
【题目】如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足( )条件时,四边形EGFH是菱形.
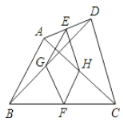
A.AB=CDB.AB//CDC.AB⊥CDD.AB=CD AB//CD
【答案】A
【解析】
E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且等于![]() AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=![]() CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
需添加条件AB=CD.
证明:∵点E,G分别是AD,BD的中点,
∴EG∥AB,且EG=![]() AB,同理HF∥AB,且HF=
AB,同理HF∥AB,且HF=![]() AB,
AB,
∴EG∥HF,EG=HF,
∴四边形EGFH是平行四边形.
∵EG=![]() AB,同理可得EH=
AB,同理可得EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故选:A.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目