Ő‚ńŅńŕ»›
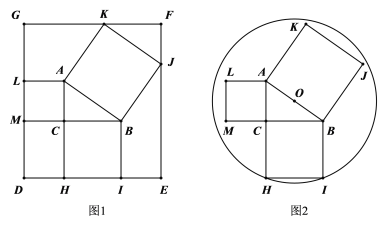
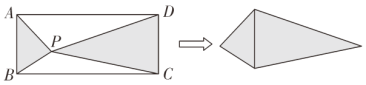
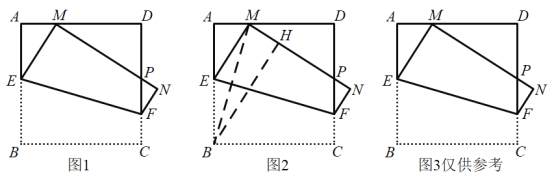
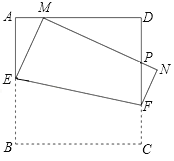
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕĪŖ≥§ő™1Ķń’ż∑Ĺ–őABCD÷–£¨∂ĮĶ„E£¨F∑÷Īū‘ŕĪŖAB£¨CD…Ō£¨Ĺę’ż∑Ĺ–őABCD—ō÷ĪŌŖEF’ŘĶĢ£¨ ĻĶ„BĶń∂‘”¶Ķ„M ľ÷’¬š‘ŕĪŖAD…Ō(Ķ„M≤Ľ”ŽĶ„A£¨D÷ōļŌ)£¨Ķ„C¬š‘ŕĶ„Nī¶£¨MN”ŽCDĹĽ”ŕĶ„P£¨…ŤBE£Ĺx£ģ
(1)ĶĪAM£Ĺ![]() Ī£¨«ůxĶń÷Ķ£Ľ
Ī£¨«ůxĶń÷Ķ£Ľ
(2)»ÁÕľ2£¨Ń¨Ĺ”BM°ĘĻżBĶ„◊ųBH°ÕMN£¨īĻ◊„ő™H£¨«ů÷§£ļBM «°ŌABHĶńĹ«∆Ĺ∑÷ŌŖ£Ľ
(3)ňś◊ŇĶ„M‘ŕĪŖAD…ŌőĽ÷√ĶńĪšĽĮ£¨°ųPDMĶń÷‹≥§ «∑Ů∑Ę…ķĪšĽĮ£Ņ»ÁĪšĽĮ£¨«ŽňĶ√ųņŪ”…£Ľ»Á≤ĽĪš£¨«Ž«ů≥Ųł√∂®÷Ķ£Ľ
(4)…ŤňńĪŖ–őBEFCĶń√śĽżő™S£¨«ůS”Žx÷ģľšĶńļĮ żĪŪīÔ Ĺ£¨≤Ę«ů≥ŲSĶń◊Ó–°÷Ķ£ģ
°ĺīūįł°Ņ£®1£©x£Ĺ![]() £ģ£®2£©÷§√ųľŻĹ‚őŲ£Ľ£®3£©≤ĽĪš£¨°ųDMPĶń÷‹≥§ő™2£Ľ£®4£©S£Ĺ
£ģ£®2£©÷§√ųľŻĹ‚őŲ£Ľ£®3£©≤ĽĪš£¨°ųDMPĶń÷‹≥§ő™2£Ľ£®4£©S£Ĺ![]() (2x£≠
(2x£≠![]() )£¨√śĽżĶń◊Ó–°÷Ķő™
)£¨√śĽżĶń◊Ó–°÷Ķő™![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©ņŻ”√ĻīĻ…∂®ņŪĻĻĹ®∑Ĺ≥Ő£¨ľīŅ…Ĺ‚ĺŲő Ő‚£Ľ
£®2£©Õ®Ļż÷§√ų°ųBAM°’°ųBHMĹÝ∂ÝŅ…Ķ√°ŌABM£Ĺ°ŌMBH£¨ľīŅ…Ķ√÷§£Ľ
£®3£©…ŤAM£Ĺy£¨‘ÚBE£ĹEM£Ĺx£¨MD£Ĺ1©Āy£¨‘ŕRt°ųAEM÷–£¨”…ĻīĻ…∂®ņŪĶ√≥Ųx°ĘyĶńĻōŌĶ Ĺ£¨Ņ…÷§Rt°ųAEM°◊Rt°ųDMP£¨łýĺ›Ōŗň∆»żĹ«–őĶń÷‹≥§Ī»Ķ»”ŕŌŗň∆Ī»«ů°ųDMPĶń÷‹≥§£Ľ
£®4£©◊ųFH°ÕAB”ŕH£ģ‘ÚňńĪŖ–őBCFH «ĺō–ő£ģѨŔBMĹĽEF”ŕO£¨ĹĽFH”ŕK£ģłýĺ›Ő›–őĶń√śĽżĻę ĹĻĻĹ®∂ĢīőļĮ ż£¨ņŻ”√∂ĢīőļĮ żĶń–‘÷ Ĺ‚ĺŲ◊Ó÷Ķő Ő‚ľīŅ…£Ľ
Ĺ‚£ļ£®1£©»ÁÕľ£¨‘ŕRt°ųAEM÷–£¨AE£Ĺ1©Āx£¨EM£ĹBE£Ĺx£¨AM£Ĺ![]() £¨
£¨
°ŖAE2+AM2£ĹEM2£¨
°ŗ£®1©Āx£©2+£®![]() £©2£Ĺx2£¨
£©2£Ĺx2£¨
°ŗx£Ĺ![]() £ģ
£ģ
£®2£©°ŖEB£ĹEM£¨
°ŗ°ŌEBM£Ĺ°ŌEMB£ģ
°Ŗ°ŌEBC£Ĺ°ŌEMN£¨
°ŗ°ŌMBC£Ĺ°ŌBMN£ģ
°ŖAD°őBC£¨
°ŗ°ŌMBC£Ĺ°ŌAMB£¨
°ŗ°ŌAMB£Ĺ°ŌBMN£¨
”÷°Ŗ°ŌA£Ĺ°ŌMHB£¨BM£ĹBM£¨
°ŗ°ųBAM°’°ųBHM£ģ
°ŗ°ŌABM£Ĺ°ŌMBH£¨
°ŗBM «°ŌABHĶńĹ«∆Ĺ∑÷ŌŖ£Ľ
£®3£©°ųDMPĶń÷‹≥§≤ĽĪš£¨ő™2£ģ
ņŪ”…£ļ…ŤAM£Ĺy£¨‘ÚBE£ĹEM£Ĺx£¨MD£Ĺ1©Āy£¨
‘ŕRt°ųAEM÷–£¨”…ĻīĻ…∂®ņŪĶ√AE2+AM2£ĹEM2£¨
°ŗ£®1©Āx£©2+y2£Ĺx2£¨
Ĺ‚Ķ√1+y2£Ĺ2x£¨
°ŗ1©Āy2£Ĺ2£®1©Āx£©
°Ŗ°ŌEMP£Ĺ90°„£¨°ŌA£Ĺ°ŌD£¨
°ŗRt°ųAEM°◊Rt°ųDMP£¨
°ŗ![]() £Ĺ
£Ĺ![]() £¨
£¨
ľī![]() £Ĺ
£Ĺ![]() £¨
£¨
Ĺ‚Ķ√DM![]() £Ĺ2£ģ
£Ĺ2£ģ
°ŗ°ųDMPĶń÷‹≥§≤ĽĪš£¨ő™2£ģ
£®4£©◊ųFH°ÕAB”ŕH£ģѨŔBMĹĽEF”ŕO£¨ĹĽFH”ŕK£ģ
‘ÚňńĪŖ–őBCFH «ĺō–ő£ģ
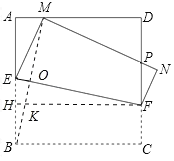
‘ŕRt°ųAEM÷–£¨AM£Ĺ![]() £Ĺ
£Ĺ![]() £¨
£¨
°ŖB°ĘMĻō”ŕEF∂‘≥∆£¨
°ŗBM°ÕEF£¨
°ŗ°ŌKOF£Ĺ°ŌKHB£¨
°Ŗ°ŌOKF£Ĺ°ŌBKH£¨
°ŗ°ŌKFO£Ĺ°ŌKBH£¨
°ŖAB£ĹBC£ĹFH£¨°ŌA£Ĺ°ŌFHE£Ĺ90°„£¨
°ŗ°ųABM°’°ųHFE£¨
°ŗEH£ĹAM£Ĺ![]() £¨
£¨
°ŗCF£ĹBH£Ĺx©Ā![]() £¨
£¨
°ŗS£Ĺ![]() £®BE+CF£©BC
£®BE+CF£©BC
£Ĺ![]() £®x+x©Ā
£®x+x©Ā![]() £©
£©
£Ĺ![]() £®2x©Ā
£®2x©Ā![]() £©
£©
£Ĺ![]() [£®
[£®![]() £©2©Ā
£©2©Ā![]() +1]
+1]
£Ĺ![]() £®
£®![]() ©Ā
©Ā![]() £©2+
£©2+![]() £ģ
£ģ
°ŗS£Ĺ![]() £®2x©Ā
£®2x©Ā![]() £©£¨
£©£¨
ĶĪ![]() £Ĺ
£Ĺ![]() Ī£¨S”–◊Ó–°÷Ķ£Ĺ
Ī£¨S”–◊Ó–°÷Ķ£Ĺ![]() £ģ
£ģ

 ‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
‘ń∂ŃŅž≥ĶŌĶŃ–īūįł