题目内容
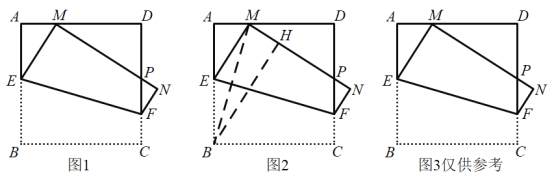
【题目】一张矩形纸板和圆形纸板按如图方式分别剪得同样大定理特例图(AC=3,BC=4,AB=5,分别以三边长向外剪正方形) ,图1中边HI、LM和点K、J都恰好在矩形纸板的边上,图2中的圆心O在AB中点处,点H、I都在圆上,则矩形和圆形纸板的面积比是( )
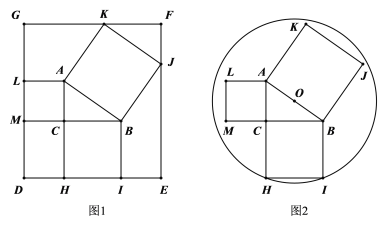
A.400:127πB.484:145πC.440:137πD.88:25π
【答案】C
【解析】
如图1(见解析),先利用正方形的性质、三角形全等的判定定理与性质可得![]() ,
,![]() ,同样的方法可得
,同样的方法可得![]() ,从而可得出DE、EF的长,再根据矩形的面积公式即可得;如图2(见解析),先根据中位线定理求出OD、CD的长,从而可得DH的长,再利用勾股定理可得
,从而可得出DE、EF的长,再根据矩形的面积公式即可得;如图2(见解析),先根据中位线定理求出OD、CD的长,从而可得DH的长,再利用勾股定理可得![]() 的值,然后根据圆的面积公式即可得,由此即可得出答案.
的值,然后根据圆的面积公式即可得,由此即可得出答案.
如图1,过点B作![]() 于点N
于点N
![]()
![]()
![]() 是直角三角形,且
是直角三角形,且![]()
![]() 四边形ABJK是正方形
四边形ABJK是正方形
![]() ,
,![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,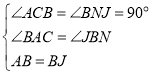
![]()
![]() ,
,![]()
同理可证:![]()
![]()
![]() 四边形BCHI是正方形
四边形BCHI是正方形
![]() ,
,![]()
![]() 四边形DEFG是矩形
四边形DEFG是矩形
![]()
![]()
![]() 四边形BNEI是矩形
四边形BNEI是矩形
![]() ,
,![]()
同理可得:![]()
![]() ,
,![]()
则矩形纸板的面积为![]()
如图2,过点O作![]() 于点D,连接OH,则
于点D,连接OH,则![]()
![]()
![]() 点O为AB的中点
点O为AB的中点
![]() OD为
OD为![]() 的中位线
的中位线
![]() ,
,![]()
![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
则圆形纸板的面积为![]()
因此,矩形和圆形纸板的面积比是![]()
故选:C.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】某学校为了了解九年级学生上学期间平均每天的睡眠情况,现从全校![]() 名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间
名九年级学生中随机抽取了部分学生,调查了这些同学上学期间平均每天的睡眠时间![]() (单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
(单位:小时),并根据调查结果列出统计表,绘制成扇形统计图,如图所示.请你根据图表提供的信息解答下列问题:
平均每天睡眠时间分组统计表
组别序号 | 睡眠时间 | 人数(频数) |
|
|
|
|
|
|
|
|
|
|
|
|
平均每天睡眠时间扇形统计表
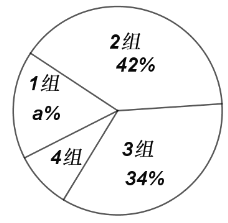
(1)![]() _______,
_______,![]() _______,
_______,![]() _______(
_______(![]() 为百分号前的数字);
为百分号前的数字);
(2)随机抽取的这部分学生平均每天睡眠时间的中位数落在_______组(填组别序号);
(3)估计全校![]() 名九年级学生中平均每天睡眠时间不低于
名九年级学生中平均每天睡眠时间不低于![]() 小时的学生有_______名;
小时的学生有_______名;
(4)若所抽查的睡眠时间![]() (小时)的
(小时)的![]() 名学生,其中
名学生,其中![]() 名男生和
名男生和![]() 名女生,现从这
名女生,现从这![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加个别访谈,请用列表或画树状图的方法求选取的
名学生参加个别访谈,请用列表或画树状图的方法求选取的![]() 名学生恰为
名学生恰为![]() 男
男![]() 女的概率.
女的概率.
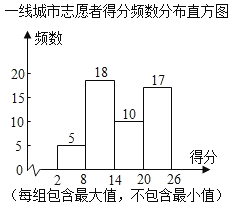
【题目】为了解疫情对精神负荷造成的影响,某机构分别在一线城市和三线城市的志愿者中随机选取了50人参加LES测试,根据志愿者的答题情况计算出LES得分,并对得分进行整理,描述和分析,部分信息如下:
一、三线城市志愿者得分统计表
城市 | 中位数 | 平均数 |
一线城市 | a | 17.6 |
三线城市 | 14 | 17.2 |
注:一线城市在14<x≤20中的得分是:15,15,16,17,17,17,17,18,18,20.
根据以上信息,解答下列问题:
(1)表中a的值为 ;
(2)得分越低反映个体承受的精神压力越小,排名越靠前,在这次调查中,一线城市的志愿者甲和三线城市的志愿者乙的得分均为15分,请判断甲、乙在各自城市选取的志愿者中得分排名谁更靠前,并说明理由;
(3)如果得分超过平均数就需要进行心理干预,请估计一线城市全部2000名志愿者中有多少人需要进行心理干预?