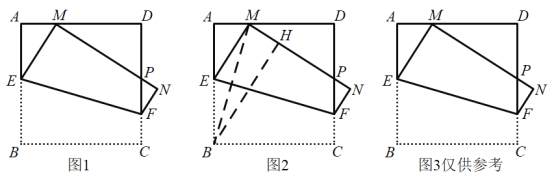
ĢāÄæÄŚČŻ
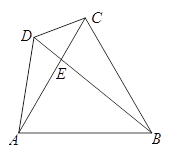
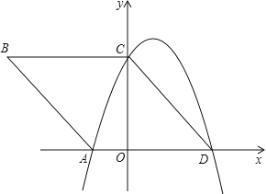
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬ĖıߊĪABCDŹĒ±ß³¤ĪŖ5µÄĮāŠĪ£¬¶„µćA£®C£®D¾łŌŚ×ų±źÖįÉĻ£¬sinB=![]() £®
£®
£Ø1£©Ēó¹żA£¬C£¬DČżµćµÄÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©¼ĒÖ±ĻßABµÄ½āĪöŹ½ĪŖy1=mx+n£¬£Ø1£©ÖŠÅ×ĪļĻߵĽāĪöŹ½ĪŖy2=ax2+bx+c£¬Ēóµ±y1>y2Ź±£¬×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø3£©ÉčÖ±ĻßABÓė£Ø1£©ÖŠÅ×ĪļĻßµÄĮķŅ»øö½»µćĪŖE£¬PµćĪŖÅ×ĪļĻßÉĻA£¬EĮ½µćÖ®¼äµÄŅ»øö¶Æµć£¬ĒŅÖ±ĻßPE½»xÖįÓŚµćF£¬ĪŹ£ŗµ±PµćŌŚŗĪ“¦Ź±£¬”÷PAEµÄĆ껿×ī“ó£æ²¢Ēó³öĆ껿µÄ×ī“óÖµ£®
”¾“š°ø”æ£Ø1£©y=©![]() x2+
x2+![]() x+4£»£Ø2£©x£¼-2»ņx£¾5£»£Ø3£©µ±P(
x+4£»£Ø2£©x£¼-2»ņx£¾5£»£Ø3£©µ±P(![]() £¬
£¬![]() )Ź±£¬”÷PAEµÄĆ껿×ī“ó£¬×ī“óĆ껿ĪŖ
)Ź±£¬”÷PAEµÄĆ껿×ī“ó£¬×ī“óĆ껿ĪŖ![]()
”¾½āĪö”æ
£Ø1£©ÓÉĮāŠĪABCDµÄ±ß³¤ŗĶŅ»½ĒµÄÕżĻŅÖµ£¬æÉĒó³öOC”¢OD”¢OAµÄ³¤£¬½ų¶ųČ·¶ØA”¢C”¢DČżµć×ų±ź£¬Ķعż“ż¶ØĻµŹż·ØæÉĒó³öÅ×ĪļĻߵĽāĪöŹ½£®
£Ø2£©Ź×ĻČÓÉA”¢BµÄ×ų±źČ·¶ØÖ±ĻßABµÄ½āĪöŹ½£¬Č»ŗóĒó³öÖ±ĻßABÓėÅ×ĪļĻß½āĪöŹ½µÄĮ½øö½»µć£¬Č»ŗóĶعż¹Ū²ģĶ¼ĻóÕŅ³öÖ±Ļßy1ŌŚÅ×ĪļĻßy2Ķ¼ĻóĻĀ·½µÄ²æ·Ö£®
£Ø3£©øĆĢāµÄ¹Ų¼üµćŹĒČ·¶ØµćPµÄĪ»ÖĆ£¬”÷APEµÄĆ껿×ī“ó£¬ÄĒĆ“S”÷APE=![]() AE”ĮhÖŠhµÄÖµ×ī“󣬼“µćPĄėÖ±ĻßAEµÄ¾ąĄė×īŌ¶£¬ÄĒĆ“µćPĪŖÓėÖ±ĻßABĘ½ŠŠĒŅÓėÅ×ĪļĻßÓŠĒŅ½öÓŠµÄĪØŅ»½»µć£®
AE”ĮhÖŠhµÄÖµ×ī“󣬼“µćPĄėÖ±ĻßAEµÄ¾ąĄė×īŌ¶£¬ÄĒĆ“µćPĪŖÓėÖ±ĻßABĘ½ŠŠĒŅÓėÅ×ĪļĻßÓŠĒŅ½öÓŠµÄĪØŅ»½»µć£®
½ā£ŗ£Ø1£©”ßĖıߊĪABCDŹĒ±ß³¤ĪŖ5µÄĮāŠĪ£¬”ąAB=AD=CD=BC=5£¬sinB=sinD=![]() £»
£»
Rt”÷OCDÖŠ£¬OC=CDsinD=4£¬OD=3£»OA=AD©OD=2£¬¼“£ŗ
A£Ø©2£¬0£©”¢B£Ø©5£¬4£©”¢C£Ø0£¬4£©”¢D£Ø3£¬0£©£»
ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗy=a£Øx+2£©£Øx©3£©£¬µĆ£ŗ2”Į£Ø©3£©a=4£¬a=![]() £»
£»
”ąÅ×ĪļĻߣŗy=©![]() x2+
x2+![]() x+4£®
x+4£®
£Ø2£©ÓÉA£Ø©2£¬0£©”¢B£Ø©5£¬4£©µĆÖ±ĻßAB£ŗy1=©![]() x©
x©![]() £»
£»
ÓÉ£Ø1£©µĆ£ŗy2=©![]() x2+
x2+![]() x+4£¬Ōņ£ŗ
x+4£¬Ōņ£ŗ
 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ £¬
£¬ £»
£»
ÓÉĶ¼æÉÖŖ£ŗµ±y1>y2Ź±£¬x&l;-2»ņx>5£®
£Ø3£©”ßS”÷APE=![]() AEh£¬”ąµ±Pµ½Ö±ĻßABµÄ¾ąĄė×īŌ¶Ź±£¬S”÷ABE×ī“ó£»
AEh£¬”ąµ±Pµ½Ö±ĻßABµÄ¾ąĄė×īŌ¶Ź±£¬S”÷ABE×ī“ó£»
ČōÉčÖ±ĻßL”ĪAB£¬ŌņÖ±ĻßLÓėÅ×ĪļĻßÓŠĒŅÖ»ÓŠŅ»øö½»µćŹ±£¬øĆ½»µć¼“ĪŖµćP£»
ÉčÖ±ĻßL£ŗy=©![]() x+b£¬µ±Ö±ĻßLÓėÅ×ĪļĻßÓŠĒŅÖ»ÓŠŅ»øö½»µćŹ±£¬
x+b£¬µ±Ö±ĻßLÓėÅ×ĪļĻßÓŠĒŅÖ»ÓŠŅ»øö½»µćŹ±£¬
©![]() x+b=©
x+b=©![]() x2+
x2+![]() x+4£¬ĒŅ”÷=0£»ĒóµĆ£ŗb=
x+4£¬ĒŅ”÷=0£»ĒóµĆ£ŗb=![]() £¬¼“Ö±ĻßL£ŗy=©
£¬¼“Ö±ĻßL£ŗy=©![]() x+
x+![]() £»
£»
æɵƵćP£Ø![]() £¬
£¬![]() £©£®ÓÉ£Ø2£©µĆ£ŗE£Ø5£¬©
£©£®ÓÉ£Ø2£©µĆ£ŗE£Ø5£¬©![]() £©£¬ŌņÖ±ĻßPE£ŗy=©
£©£¬ŌņÖ±ĻßPE£ŗy=©![]() x+9£»
x+9£»
PEÓėxÖįµÄ½»µćFµÄ×ų±źĪŖ£Ø![]() £¬0£©£¬AF=OA+OF=
£¬0£©£¬AF=OA+OF=![]() £»
£»
”ą”÷PAEµÄ×ī“óÖµ£ŗS”÷PAE=S”÷PAF+S”÷AEF=![]() ”Į
”Į![]() ”Į£Ø
”Į£Ø![]() +
+![]() £©=
£©=![]() £®
£®
×ŪÉĻĖłŹö£¬µ±P£Ø![]() £¬
£¬![]() £©Ź±£¬”÷PAEµÄĆ껿×ī“ó£¬×ī“óĆ껿ĪŖ
£©Ź±£¬”÷PAEµÄĆ껿×ī“ó£¬×ī“óĆ껿ĪŖ![]() £®
£®

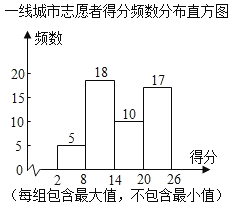
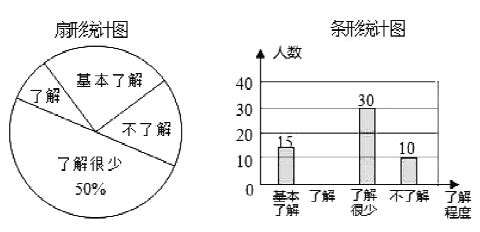
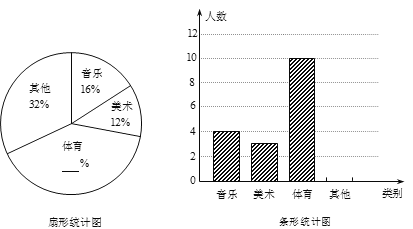
”¾ĢāÄæ”æĪŖĮĖ½āŅßĒé¶Ō¾«ÉńøŗŗÉŌģ³ÉµÄÓ°Ļģ£¬Ä³»ś¹¹·Ö±šŌŚŅ»Ļß³ĒŹŠŗĶČżĻß³ĒŹŠµÄÖ¾ŌøÕßÖŠĖ껜єȔĮĖ50ČĖ²Ī¼ÓLES²āŹŌ£¬øł¾ŻÖ¾ŌøÕߵēšĢāĒéæö¼ĘĖć³öLESµĆ·Ö£¬²¢¶ŌµĆ·Ö½ųŠŠÕūĄķ£¬ĆčŹöŗĶ·ÖĪö£¬²æ·ÖŠÅĻ¢ČēĻĀ£ŗ
Ņ»”¢ČżĻß³ĒŹŠÖ¾ŌøÕߵƷÖĶ³¼Ę±ķ
³ĒŹŠ | ÖŠĪ»Źż | Ę½¾łŹż |
Ņ»Ļß³ĒŹŠ | a | 17.6 |
ČżĻß³ĒŹŠ | 14 | 17.2 |
×¢£ŗŅ»Ļß³ĒŹŠŌŚ14£¼x”Ü20ÖŠµÄµĆ·ÖŹĒ£ŗ15£¬15£¬16£¬17£¬17£¬17£¬17£¬18£¬18£¬20£®
øł¾ŻŅŌÉĻŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±ķÖŠaµÄÖµĪŖ””””””””£»
£Ø2£©µĆ·ÖŌ½µĶ·“Ó³øöĢ峊ŹÜµÄ¾«ÉńŃ¹Į¦Ō½Š”£¬ÅÅĆūŌ½ææĒ°£¬ŌŚÕā“Īµ÷²éÖŠ£¬Ņ»Ļß³ĒŹŠµÄÖ¾ŌøÕß¼×ŗĶČżĻß³ĒŹŠµÄÖ¾ŌøÕßŅŅµÄµĆ·Ö¾łĪŖ15·Ö£¬ĒėÅŠ¶Ļ¼×”¢ŅŅŌŚø÷×Ō³ĒŹŠŃ”Č”µÄÖ¾ŌøÕßÖŠµĆ·ÖÅÅĆūĖøüææĒ°£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©Čē¹ūµĆ·Ö³¬¹żĘ½¾łŹż¾ĶŠčŅŖ½ųŠŠŠÄĄķøÉŌ¤£¬Ēė¹Ą¼ĘŅ»Ļß³ĒŹŠČ«²æ2000ĆūÖ¾ŌøÕßÖŠÓŠ¶ąÉŁČĖŠčŅŖ½ųŠŠŠÄĄķøÉŌ¤£æ